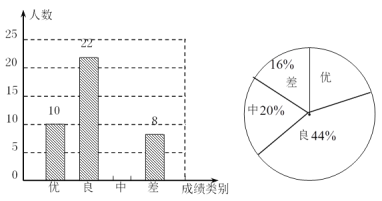
题目内容
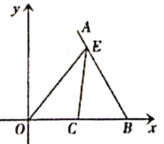
【题目】如图,某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验,先在公路旁选一点C,再在笔直的车道a上确定点D,使CD⊥a,测得CD=42米,在a上点D的同侧取点A、B,使∠CAD=30 o,∠CBD=45o.
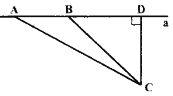
(1)求AB的长(结果保留根号);
(2)若本路段对汽车限速为60km/h,现测得某汽车从A到B用时2秒,这辆汽车是否超速?说明理由.(参考数据![]() )
)
【答案】(1)AB的长![]() ;(2)v=55.2<60,不超速.理由见解析.
;(2)v=55.2<60,不超速.理由见解析.
【解析】
(1)在Rt△ACD中求出AD,在Rt△BCD中求出BD,继而可得出AB的长度;
(2)根据速度=路程÷时间,求出速度,继而比较可判断是否超速.
解:(1)在Rt△ACD中,CD=42米,∠CAD=30°,
∴AD=![]() =
=![]() 米,
米,
在Rt△BCD中,CD=42米,∠CBD=45°,
∴AD=![]() =42米,
=42米,
∴AB=AD-BD=![]() 米;
米;
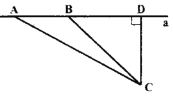
(2)汽车行驶车速= ![]() m/s≈55.2km/h,
m/s≈55.2km/h,
∵55.2<60,
∴这辆车没有超速.

【题目】多肉植物由于体积小、外形萌,近年来受到广大养花爱好者的青睐.创业青年小宇利用这个商机,去花卉市场选购各种多肉,了解到甲、乙、丙三种多肉的部分价格如下表.
多肉种类 价格 | 甲 | 乙 | 丙 |
批发价(元/株) |
| ||
零售价(元/株) |
|
|
|
(1)已知小宇第一次批发购进甲多肉![]() 株,乙多肉
株,乙多肉![]() 株,共花费
株,共花费![]() 元,且甲多肉每株的批发价比乙多肉低
元,且甲多肉每株的批发价比乙多肉低![]() 元,求甲多肉、乙多肉每株的批发价.
元,求甲多肉、乙多肉每株的批发价.
(2)由于销量好,第一次多肉全部售完,小宇用第一次的销售收入再批发甲、乙、丙三种多肉,且购进甲、乙多肉的株数相等,但乙多肉的批发价每株比原来降低![]() ,甲多肉的批发价,每株比原来提高
,甲多肉的批发价,每株比原来提高![]() .
.
①若他第二次批发购进甲、乙两种多肉分别花费![]() 元、
元、![]() 元,求
元,求![]() 的值.
的值.
②在![]() 的值不变的前提下,小宇把第一次的销售收入全用于第二次多肉批发,若第二次销售完这三种多肉所得利润为
的值不变的前提下,小宇把第一次的销售收入全用于第二次多肉批发,若第二次销售完这三种多肉所得利润为![]() 元,当丙多肉的株数不少于
元,当丙多肉的株数不少于![]() 时,求
时,求![]() 的最大值.
的最大值.