题目内容
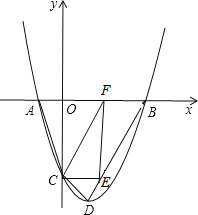
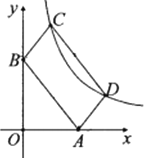
【题目】如图，在平面直角坐标系中，反比例函数
的图象经过□
的顶点
，
若点
的坐标分别为
，
，点的横坐标和纵坐标之和为
，则
的值为（ ）
A.
B.
C.
D.
【答案】D
【解析】
由已知可设C（x,7.5-x），根据平移的性质可得D（3+x,7.5-x-4），再根据反比例函数性质得x(7.5-x)=(3+x)(3.5-x)，再求k= x（7.5-x）.
因为点C的横坐标和纵坐标之和为7.5，
所以可设C（x,7.5-x）
因为四边形ABCD是平行四边形
所以AB平移可得CD，A的对应点是D
所以D（3+x,7.5-x-4），即D（3+x,3.5-x）
因为C,D在反比例函数图象上
所以x(7.5-x)=(3+x)(3.5-x)
解得x=1.5
所以7.5-x=6
所以k= x（7.5-x）=9
故答案为：D
练习册系列答案
相关题目
【题目】多肉植物由于体积小、外形萌，近年来受到广大养花爱好者的青睐．创业青年小宇利用这个商机，去花卉市场选购各种多肉，了解到甲、乙、丙三种多肉的部分价格如下表．
多肉种类 价格 | 甲 | 乙 | 丙 |
批发价（元/株） |
| ||
零售价（元/株） |
|
|
|
（1）已知小宇第一次批发购进甲多肉
株，乙多肉
株，共花费
元，且甲多肉每株的批发价比乙多肉低
元，求甲多肉、乙多肉每株的批发价．
（2）由于销量好，第一次多肉全部售完，小宇用第一次的销售收入再批发甲、乙、丙三种多肉，且购进甲、乙多肉的株数相等，但乙多肉的批发价每株比原来降低
，甲多肉的批发价，每株比原来提高
．
①若他第二次批发购进甲、乙两种多肉分别花费
元、
元，求
的值．
②在的值不变的前提下，小宇把第一次的销售收入全用于第二次多肉批发，若第二次销售完这三种多肉所得利润为
元，当丙多肉的株数不少于
时，求
的最大值．
