题目内容
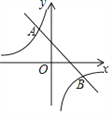
【题目】在直角坐标系中,一条直线经过A(﹣1,5),P(2,a),B(3,﹣3).
(1)求直线AB的函数表达式;
(2)求a的值;
(3)求△AOP的面积.
【答案】(1)y=﹣2x+3;(2)a=﹣1;(3)4.5.
【解析】
(1)根据点A、B的坐标利用待定系数法即可求出直线AB的解析式;
(2)利用一次函数图象上点的坐标即可求出a值;
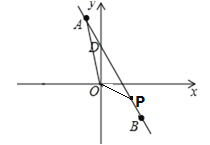
(3)设AB与y轴交与点D,将x=0代入直线AB的解析式中求出点D的坐标,再根据S△AOP=S△AOD+S△POD利用三角形的面积公式即可得出结论.
解:(1)设直线AB的函数表达式为y=kx+b,把点A、B的坐标代入得:![]() ,
,
解得:k=﹣2,b=3,所以直线AB的函数解析式为y=﹣2x+3;
(2)把P(2,a)代入y=﹣2x+3得:a=﹣1;
(3)
∵把x=0代入y=﹣2x+3得:y=3,
∴直线y=﹣2x+3与y轴的交点为(0,3),即OD=3,
∵P(2,﹣1),
∴△AOP的面积=△AOD的面积+△DOP的面积=![]() +
+![]() =4.5.
=4.5.
故答案为:(1)y=﹣2x+3;(2)a=﹣1;(3)4.5.

练习册系列答案
相关题目