题目内容
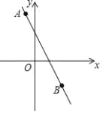
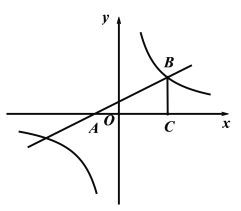
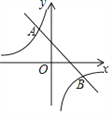
【题目】如图,一次函数y=k1x+b与反比例函数y=![]() 的图象交于点A(m,2),B(2,-1).
的图象交于点A(m,2),B(2,-1).
(1)求这两个函数的表达式;
(2)在x轴上是否存在点P(n,0),使△ABP为直角三角形,请你直接写出P点的坐标.
【答案】(1)![]() ;y=-x+1;(2)P点的坐标(3,0)、(﹣3,0)、(
;y=-x+1;(2)P点的坐标(3,0)、(﹣3,0)、(![]() ,0)或(
,0)或(![]() ,0).
,0).
【解析】分析:(1)把点B坐标代入y=![]() 求出反比例函数的解析式,再把点A坐标代入反比例函数的解析式求出m的值,利用待定系数法求出一次函数解析式.
求出反比例函数的解析式,再把点A坐标代入反比例函数的解析式求出m的值,利用待定系数法求出一次函数解析式.
(2)分三种情况进行讨论, ①当∠BAP=90°; ②当∠BPA=90°; ③当∠PBA=90°, 利用勾股定理的逆定理建立方程即可得出结论.
详解: (1)把A(1,2)代入y=![]() 得:2=k 1
得:2=k 1
∴k =2×(1)=2
∴![]()
把B(m,2)代入![]() 得:m=-1,
得:m=-1,
∴B(-1,2)
把A(1,2),B(2,1)分别代入y=k x+b得:
![]()
∴![]()
∴y=x+1
(2)∵A(1,2),B(2,1),P(n,0),
∴AB =18,AP =(n+1) +4,BP =(n2) +1,
∵△ABP为直角三角形,
∴①当∠ABP=90°时,AB +BP =AP ,
∴18+(n2) +1=(n+1) +4,
∴n=3,
∴P(3,0),
②当∠BAP=90°时,AB +AP =BP ,
∴18+(n+1) +4=(n2) +1,
∴n=3,
∴P(3,0),
③当∠APB=90°时,AP +BP =AB ,
∴(n+1) +4+(n2) +1=18,
∴n=![]() ,
,
∴P(![]() ,0)或(
,0)或(![]() ,0)
,0)
即:P点的坐标(3,0)、(3,0)、(![]() ,0)或(
,0)或(![]() ,0).
,0).
点睛: 本题考查反比例函数和一次函数解析式的确定、等腰直角三角形的判定等知识及综合应用知识、解决问题的能力.要注意在不确定直角三角形的直角边和底边的情况下要考虑到所有的情况,不要漏解.

 新思维寒假作业系列答案
新思维寒假作业系列答案