题目内容
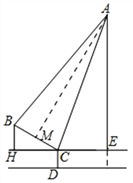
【题目】如图1,图2,分别是吊车在吊一物品时的实物图与示意图,已知吊车底盘CD的高度为1.8米,支架BC的长为4米,且与地面成30°角,吊绳AB与支架BC的夹角为80°,吊臂AC与地面成70°角,求吊车的吊臂顶端A点距地面的高度是多少米?(精确到0.1米,参考数据:sin10°=cos80°=0.17,cos10°=sin80°=0.98,sin20°=cos70°=0.34,tan70°=2.75,sin70°=0.94)

【答案】点A到地面的距离为12.9米.
【解析】试题分析:过点A作AM⊥BC于M,先证明∠ABC=∠ACB,推出AB=AC.在Rt△ACM中,求出AC,再在Rt△ACE中求出AE即可解决问题.
试题解析:解:由题可知,BH⊥HE,AE⊥HE,CD=2米,BC=4米,∠BCH=30°,∠ABC=80°,∠ACE=70°.∵∠BCH+∠ACB+∠ACE=180°,∴∠ACB=80°.
∵∠ABC=80°,∴∠ABC=∠ACB,∴AB=AC.
过点A作AM⊥BC于M,则CM=BM=2米.
∵在Rt△ACM中,CM=2米,∠ACB=80°,∴![]() =cos∠ACB=cos80°≈0.17,∴AC=
=cos∠ACB=cos80°≈0.17,∴AC=![]() =
=![]() (米).∵在Rt△ACE中,AC=
(米).∵在Rt△ACE中,AC=![]() ,∠ACE=70°,∴
,∠ACE=70°,∴![]() =sin∠ACE=sin70°≈0.94,
=sin∠ACE=sin70°≈0.94,
∴AE=![]() ×0.94=
×0.94=![]() ≈11.1(米),11.1+2=13.1(米)
≈11.1(米),11.1+2=13.1(米)
故点A到地面的高度为13.1米.

练习册系列答案
相关题目