题目内容
【题目】如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需绕行B地,现计划开凿隧道使A、C两地直线贯通,经测量得:B地在A地的北偏东67°方向,距离A地280km,C地在B地南偏东的30°方向.
(1)求B地到直线AC的距离;
(2)求隧道开通后与隧道开通前相比,从A地到C地的路程将缩短多少?
(本题结果都精确到0.1km)
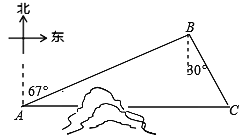
【答案】(1)B地到直线AC的距离约为109.4km;(2)隧道开通后与隧道开通前相比,从A地到C地的路程将缩短85.4km.
【解析】分析:(1)作BD⊥AC于点D,在直角△ABD中求解BD即可;
(2)分别求得AD、CD、BC的长,利用AD+CD-(AB+BC)即可.
详解:(1)如图,作BD⊥AC于点D,

在Rt△ABD中,∠ABD=67°,AB=280
∵![]() ,
,
∴![]()
答:B地到直线AC的距离约为109.4km.
(2)∵ ![]()
∴![]()
在Rt△BCD中,∠CBD=30°BD=109.4,
∴![]()
![]()
∴![]()
∴ ![]()
答:隧道开通后与隧道开通前相比,从A地到C地的路程将缩短85.4km.
点睛: 本题考查的是解直角三角形的应用-方向角问题,熟记锐角三角函数的定义是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目