Question

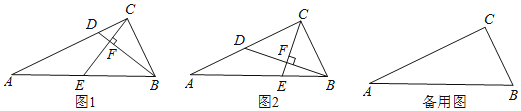
【题目】如图，Rt△ABC中，∠ACB＝90°，tanA＝，D、E分别在AC、AB边上，BD⊥CE于F．

（1）如图1，若E是AB的中点，求证：CE＝BD；

（2）如图2，若＝，求tan∠ABD；

（3）BC＝2，P点在AC边上运动，请直接写出BP+AP的最小值为　 　．

Answer 1

【答案】（1）证明见解析；（2）tan∠ABD＝；（3）

【解析】

（1）过点E作EG⊥AC于G，先判断出AC＝2BC，再判断出EG是△ABC的中位线，得出AC＝2CG，进而得出BC＝CG，判断出△CEG≌△BDC，即可得出结论；

（2）先判断出△CGE∽△BCD，设出CG＝2m，BC＝3m，进而表示出AG＝4m，再用三角函数表示出EG，CD，进而表示出AD，进而借助勾股定理表示出DH，BH，即可得出结论；

（3）先作出PH＝PG＝AP，进而得出当点B，P，H在同一条线上时，BP+PH最小，判断出AP＝BP，再求出AN＝PN＝AB＝，进而求出AP＝，即可得出结论．

（1）证明：过点E作EG⊥AC于G，

在Rt△ABC中，tanA＝＝，

∴AC＝2BC，

∵∠ACB＝90°，

∴∠GCE+∠BCE＝90°，

∵BD⊥CE，

∴∠BCE+∠CBD＝90°，

∴∠GCE＝∠CBD，

∴∠CGE＝90°＝∠ACB，

∴EG∥BC，

∵点E是AB的中点，

∴EG是△ABC的中位线，

∴AC＝2CG，

∴BC＝CG，

∴△CEG≌△BDC（ASA），

∴CE＝BD；

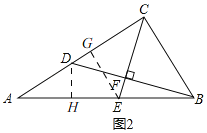
（2）如图2，由（1）知，AC＝2BC，根据勾股定理得，AB＝BC，

过点E作EG⊥AC于G，

∴∠CGE＝∠BCD＝90°，

同（1）的方法得，∠ECG＝∠DCB，

∴△CGE∽△BCD，

∴，

∵，

∴，

设CG＝2m，BC＝3m，

∴AB＝3m，AC＝6m，

∴AG＝AC﹣CG＝4m，

在Rt△AGE中，tanA＝＝，

∴EG＝AG＝2m，

∴CD＝3m，

∴AD＝AC﹣CD＝3m，

过点D作DH⊥AB于H，tanA＝＝，

设DH＝n，AH＝2n，根据勾股定理得，n＝3m，

∴n＝m

∴DH＝m，AH＝m，

∴BH＝AB﹣AH＝m，

在Rt△DHB中，tan∠ABD＝＝．

（3）在Rt△ABC中，tanA＝＝，BC＝2，

∴AC＝4，根据勾股定理得，AB＝2，

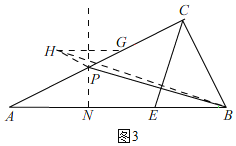
如图3，过点P作PN⊥AB交AB于N，

在AP的延长线上取一点G，使PG＝AP，作点G关于PN的对称点H，连接PH，此时，PH＝PG＝AP，

∴BP+AP＝BP+PH，

当点B，P，H在同一条线上时，BP+PH最小，

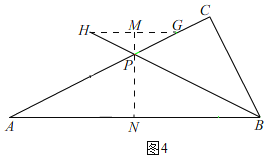
如图4，

由对性知，PH＝PG，

∴∠H＝∠PGH，

∵GH⊥PN，

∴HG∥AB，

∴∠A＝∠PGH，∠ABP＝∠H，

∴∠A＝∠ABP，

∴PA＝PB，

∵PN⊥AB，

∴AN＝PN＝AB＝，

在Rt△APN中，tanA＝＝，

∴PN＝AN＝，根据勾股定理得，AP＝，

∴（BP+AP）最小＝BP+PG＝BP+AP＝AP+AP＝AP＝，

故答案为．