题目内容
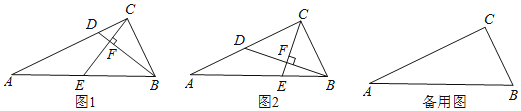
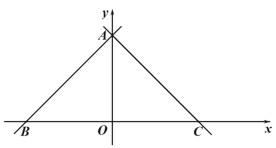
【题目】如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角.
实验与操作:根据要求进行尺规作图,并在图中标明相应字母(保留作图痕迹,不写作法)
(1)作∠DAC的平分线AM;
(2)作线段AC的垂直平分线,与AM交于点F,与BC边交于点E,连接AE、CF
探究与猜想:若∠BAE=36°,求∠B的度数.
【答案】(1)详见解析;(2)48°
【解析】
(1)利用基本作图作AM平分∠DAC;
(2)先画出几何图形,再证明∠B=∠2=∠3=∠1,接着根据线段垂直平分线的性质的EA=EC,所以∠3=∠EAC,然后利用平角的定义计算出∠1=48°,从而得到∠B的度数.
解:(1)如图,AM为所作;
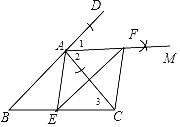
(2)∵AB=AC,
∴∠B=∠3,
∵AM平分∠DAC,
∴∠1=∠2,
而∠DAC=∠B+∠3,
∴∠B=∠2=∠3=∠1,
∴EF垂直平分AC,
∴EA=EC,
∴∠3=∠EAC,
∵∠1+∠2+∠EAC+∠BAE=180°,
∴∠1=![]() (180°﹣36°)=48°,
(180°﹣36°)=48°,
∴∠B=48°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目