题目内容
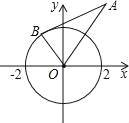
【题目】如图,⊙O的半径为2,点A的坐标为(2,2![]() ),直线AB为⊙O的切线,B为切点.则B点的坐标为( )
),直线AB为⊙O的切线,B为切点.则B点的坐标为( )
A. (﹣![]() ,
,![]() ) B. (﹣
) B. (﹣![]() ,1) C. (﹣
,1) C. (﹣![]() ,
,![]() ) D. (﹣1,
) D. (﹣1,![]() )
)
【答案】D
【解析】
过B作BE⊥x轴于E,过A作AD⊥x轴于D,求出∠AOD=60°,根据HL证Rt△ABO≌Rt△ADO,求出∠AOB=60°,求出∠BOE=60°,求出∠EBO=30°,根据OB=2,求出OE、BE即可.
过B作BE⊥x轴于E,过A作AD⊥x轴于D,
∵A(2,2![]() ),
),
∴OD=2=OB,AD=2![]() ,
,
在Rt△AOD中,tan∠AOD=![]() =
=![]() =
=![]() ,
,
∴∠AOD=60°,
∵AD⊥x轴,AB切O于B,
∴∠ADO=∠ABO=90°,
在Rt△ABO和Rt△ADO中
![]() ,
,
∴Rt△ABO≌Rt△ADO,
∴∠AOD=∠AOB=60°,
∴∠BOE=60°,
∴∠EBO=30°,
∴OE=1,
由勾股定理得:BE=![]() ,
,
∴B(1, ![]() ),
),
故答案选D.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目