题目内容
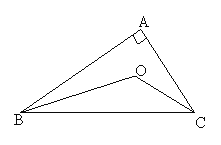
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G,F为AB边上﹣点,连接CF,且∠ACF=∠CBG.
(1)求证:AF=CG;
(2)写出图中长度等于2DE的所有线段.
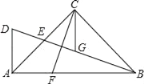
【答案】(1)详见解析;(2)长度等于2DE的线段有CF、BG、DG.
【解析】
(1)要证AF=CG,只需证明△AFC≌△CBG即可.
(2)延长CG交AB于H,则CH⊥AB,H平分AB,继而证得CH∥AD,得出DG=BG和△ADE与△CGE全等,从而证得CF=2DE.
证明:(1)∵∠ACB=90°,CG平分∠ACB,
∴∠ACG=∠BCG=45°,
又∵∠ACB=90°,AC=BC,
∴∠CAF=∠CBF=45°,
∴∠CAF=∠BCG,
在△AFC与△CGB中,
![]() ,
,
∴△AFC≌△CBG(ASA),
∴AF=CG;
(2)延长CG交AB于H,
∵CG平分∠ACB,AC=BC,
∴CH⊥AB,CH平分AB,
∵AD⊥AB,
∴AD∥CG,
∴∠D=∠EGC,
在△ADE与△CGE中,
![]() ,
,
∴△ADE≌△CGE(AAS),
∴DE=GE,
即DG=2DE,
∵AD∥CG,CH平分AB,
∴DG=BG,
∵△AFC≌△CBG,
∴CF=BG,
∴CF=2DE.
∵BG=CF,
∴BG=2DE,
∴DG=2DE,
故长度等于2DE的线段有CF、BG、DG.

练习册系列答案
相关题目