题目内容
【题目】某物体从P点运动到Q点所用时间为7秒,其运动速度v(米每秒)关于时间t(秒)的函数关系如图所示.某学习小组经过探究发现:该物体前进3秒运动的路程在数值上等于矩形AODB的面积.由物理学知识还可知:该物体前t(3<t≤7)秒运动的路程在数值上等于矩形AODB的面积与梯形BDNM的面积之和. 根据以上信息,完成下列问题: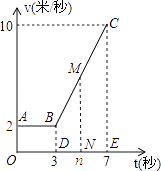
(1)当3<t≤7时,用含t的式子表示v;
(2)分别求该物体在0≤t≤3和3<t≤7时,运动的路程s(米)关于时间t(秒)的函数关系式;并求该物体从P点运动到Q总路程的 ![]() 时所用的时间.
时所用的时间.
【答案】
(1)解:设直线BC的解析式为v=kt+b,由题意,得
![]() ,
,
解得: ![]()
用含t的式子表示v为v=2t﹣4
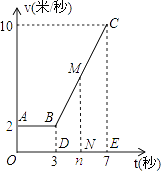
(2)解:由题意,得
根据图示知,当0≤t≤3时,S=2t;
当3<t≤7时,S=6+ ![]() (2+2t﹣4)(t﹣3)=t2﹣4t+9.
(2+2t﹣4)(t﹣3)=t2﹣4t+9.
综上所述,S= ![]() ,
,
∴P点运动到Q点的路程为:72﹣4×7+9=49﹣28+9=30,
∴30× ![]() =21,
=21,
∴t2﹣4t+9=21,
整理得,t2﹣4t﹣12=0,
解得:t1=﹣2(舍去),t2=6.
故该物体从P点运动到Q点总路程的 ![]() 时所用的时间为6秒.
时所用的时间为6秒.
【解析】(1)设直线BC的解析式为v=kt+b,运用待定系数法就可以求出t与v的关系式;(2)由路程=速度×时间,就可以表示出物体在0≤t≤3和3<t≤7时,运动的路程s(米)关于时间t(秒)的函数关系式,根据物体前t(3<t≤7)秒运动的路程在数值上等于矩形AODB的面积与梯形BDNM的面积之和求出总路程,然后将其 ![]() 代入解析式就可以求出t值.
代入解析式就可以求出t值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目