题目内容
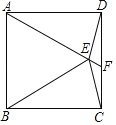
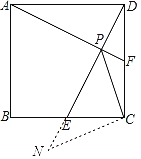
【题目】如图,正方形ABCD中,点E为边BC的上一动点,作AF⊥DE交DE、DC分别于P、F点,连PC
(1)若点E为BC的中点,求证:F点为DC的中点;
(2)若点E为BC的中点,PE=6,PC=![]() ,求PF的长.
,求PF的长.

【答案】(1)证明见解析;(2)2
【解析】
(1)先证得△ADF≌△DCE,推出DF=CE,由EC=![]() BC,BC=DC,继而可得DF=
BC,BC=DC,继而可得DF=![]() DC,即可求证结论;
DC,即可求证结论;
(2)延长PE到N,使得EN=PF,连接CN,易证△CEN≌△CFP,继而推出△NCP是等腰直角三角形,推出PN=PE+NE=PE+PF=![]() ,即可求解.
,即可求解.
证明:(1)∵四边形ABCD是正方形,
∴AD=CD=BC,∠ADC=∠C=90°,
∵AF⊥DE,
∴∠APD=∠DPF=90°,
∴∠ADP+∠DAF=90°,∠ADP+∠EDC=90°,
∴∠DAF=∠EDC,
在△ADF和△DCE中,
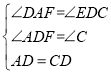 ,
,
∴△ADF≌△DCE(AAS),
∴DF=CE,
∵EC=![]() BC,BC=DC,
BC,BC=DC,
∴DF=![]() DC,
DC,
∴F点为DC的中点;
(2)延长PE到N,使得EN=PF,连接CN,
∵∠AFD=∠DEC,
∴∠CEN=∠CFP,
又∵E,F分别是BC,DC的中点,
∴CE=CF,
∵在△CEN和△CFP中
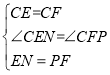 ,
,
∴△CEN≌△CFP(SAS),
∴CN=CP,∠ECN=∠PCF,
∵∠PCF+∠BCP=90°,
∴∠ECN+∠BCP=∠NCP=90°,
∴△NCP是等腰直角三角形,
∴PN=PE+NE=PE+PF=![]() ,
,
∴PF=![]() ﹣PE=8﹣6=2.
﹣PE=8﹣6=2.

练习册系列答案
相关题目