题目内容
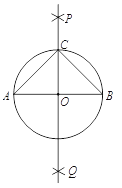
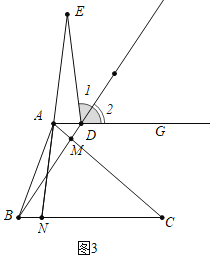
【题目】已知![]() 是等腰三角形,
是等腰三角形,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上(点
上(点![]() 不与所在线段端点重合),
不与所在线段端点重合),![]() ,连接
,连接![]() ,射线
,射线![]() ,延长
,延长![]() 交射线
交射线![]() 于点
于点![]() ,点
,点![]() 在直线
在直线![]() 上,且
上,且![]() .
.
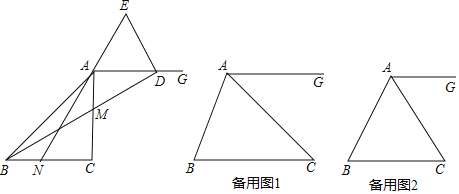
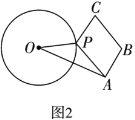
(1)如图,当![]() 时,请直接写出
时,请直接写出![]() 与
与![]() 的关系:_____;
的关系:_____;![]() 与
与![]() 的位置关系:_____.
的位置关系:_____.
(2)当![]() ,其他条件不变时,
,其他条件不变时,![]() 的度数是多少?(用含
的度数是多少?(用含![]() 的代数式表示)
的代数式表示)
(3)若![]() 是等边三角形,
是等边三角形,![]() ,
,![]() 是
是![]() 边上的三等分点,直线
边上的三等分点,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() 的长为
的长为![]() 或
或![]()
【解析】
(1)根据SAS证明![]() 即可;根据平行线的性质和余角的性质证明∠ADE+∠ADB=90°即可;
即可;根据平行线的性质和余角的性质证明∠ADE+∠ADB=90°即可;
(2)分两种情形讨论求解即可,①如图2中,当点E在AN的延长线上;②如图3中,当点E在NA的延长线上;结合外角的性质求解;
(3)分两种情形求解即可,①如图4中,当BN=![]() BC=
BC=![]() 时,作AK⊥BC于K,证明△AKN≌△DCF即可得出结论;②如图5中,当CN=
时,作AK⊥BC于K,证明△AKN≌△DCF即可得出结论;②如图5中,当CN=![]() BC=
BC=![]() 时,作AK⊥BC于K,DH⊥BC于H,证明△AKN≌△DHF即可得出结论.
时,作AK⊥BC于K,DH⊥BC于H,证明△AKN≌△DHF即可得出结论.
解:(1)证明:如图1中,∠ACB=90°,
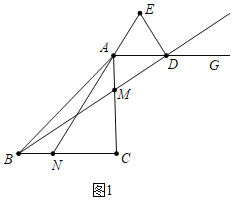
![]() ,
,![]() ,
,
![]()
即![]() ,
,
![]() ,
,
在△BCM和△ACN中,
 ,
,
![]() (SAS);
(SAS);
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
即BD与DE的位置关系为:BD⊥DE;
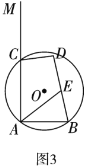
(2)解:如图2中,当点![]() 在
在![]() 的延长线上时,
的延长线上时,
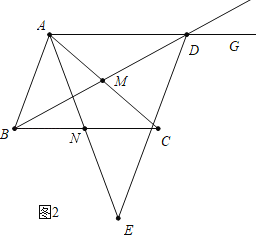
∵AG∥BC,
∠ANB=∠CAN+∠ACB=∠EAD=∠CAN+∠CAD,
∴![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
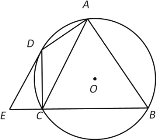
如图3中,当点![]() 在
在![]() 的延长线上时,
的延长线上时,
可得![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
综上所述,![]() 或
或![]() .
.
故答案为:![]() 或
或![]() ;
;
(3)解:如图4中,当![]() 时,作
时,作![]() 于
于![]() .
.
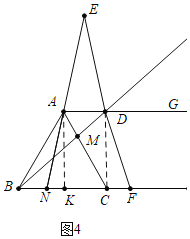
![]() ,
,
![]()
![]() ,
,
![]() =
=![]() BC,
BC,![]() ,
,
∴KC=AD,
∴四边形AKCD为平行四边形,而AK⊥KC,
则四边形![]() 是矩形,
是矩形,
∵AE=DE,
∴∠EAD=∠EDA,
∵AG∥BC,
∴∠EAD=∠ANK=∠DFC=∠EDA,
在△AKN和△DCF中,
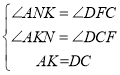
∴△AKN≌△DCF(AAS),
![]() ;
;
如图5中,当![]() 时,作
时,作![]() 于
于![]() ,
,![]() 于
于![]() .
.
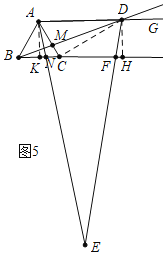
![]() ,
,
![]()
![]() ,
,
![]() ,
,
∵AK⊥AD,DH⊥AD,AG∥BC,
∴四边形AKHD为矩形,
∴AK=DH,AD=KH,
∵△ABC为等边三角形,AK⊥BC,
∴BK=CK=![]() ,
,
∴AK=![]() ,
,
则![]() ,
,
∵AE=DE,
∴∠EAD=∠EDA,
∴∠KAN=∠HDF,
在△AKN和△DHF中,
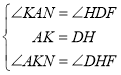 ,
,
∴![]() (ASA),
(ASA),
∴![]() ,
,
![]() .
.
综上所述,![]() 的长为
的长为![]() 或
或![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案