��Ŀ����
����Ŀ����ѧ����
�����������������У��������һ�������εĵױ߳��͵ǵĶ����ֱ������һ�������ε������Ͷ��ǵĶ�������ô�����������������λ�Ϊ��������Σ�
��������
��1����ͼ�٣�����ABC�У�AB��AC������ֱ�ߺ�Բ������������������Σ�������ͼ�ۼ�����д��������
��������
��2��������ABC�У�AB��AC����A��30����![]() ����������������εĶ��ǵĶ�����������
����������������εĶ��ǵĶ�����������
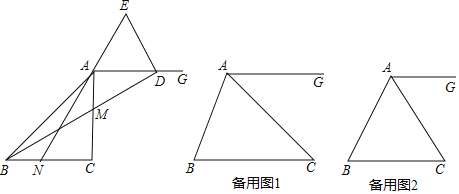
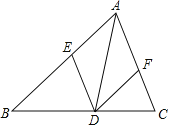
����ͼ�ڣ�����ABC�У�AB��AC��D��AC��һ�㣬����BD������ABC����ABD��Ϊ��������Σ�����ABC�ס�BCD�����A���� ������
�����о�
��3�����й�����������εĽ��ۣ�
��ÿһ�����������ζ�����������Σ�
�ڵ��������ε��������������������Σ�
������������������λ�Ϊ��������Σ���ô�����������ο���ȫ�ȣ�
�����һ�����������δ���������ͬ����������Σ���ô������������Ҳһ����Ϊ��������Σ�
����������ȷ���۵�������� ����
���𰸡���1������������2������ABC����������εĶ���Ϊ75��ʱ������Ϊ![]() ������Ϊ120��ʱ������Ϊ
������Ϊ120��ʱ������Ϊ![]() ���ڡ�A����36��������3��������ȷ���۵���������٢ۡ���
���ڡ�A����36��������3��������ȷ���۵���������٢ۡ���
��������
��1��������������εĶ��廭��ͼ�μ��ɣ�
��2���ٹ���B��BG��AC������ΪG����BG��x����취�������̽�����⼴�ɣ�
������֤����A����ABD����BDC����C����ABC�����A��x�������������ڽǺͶ����������̼��ɽ�����⣻
��3��������������εĶ���һһ�жϼ��ɣ�
��1����ͼ����DEF��Ϊ����
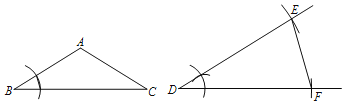
��2��������ABC�������������DEF����DE��DF��
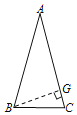
������ABC��AB��AC����A��30����BC��![]() ��
��![]() ��
��
���B����C��75����
����B��BG��AC������ΪG����BG��x��
��AB��AC��2x��AG��![]() x��
x��
��CG��AC��AG��2x��![]() x����2��
x����2��![]() ��x��
��x��
��Rt��BGC��BG2+CG2��BC2��
��x2+��2��![]() ��2x2����
��2x2����![]() ��
��![]() ��2��
��2��
��x��1��
��AB��AC��2��
��һ�����Σ���D����ABC��75����
DE��DF��BC��![]() ��
��![]() ��
��
�ڶ������Σ�����E����A��30��ʱ����EDF��120����
EF��AB��2��
����D��DH��EF������ΪH��
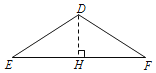
��DE��DF����EH��![]() EF��1��
EF��1��
��ED��![]() ��
��
���ABC����������εĶ���Ϊ75��ʱ������Ϊ![]() ��
��![]() ������Ϊ120��ʱ������Ϊ
������Ϊ120��ʱ������Ϊ![]() ��
��
����ͼ���У�
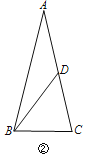
�ߡ�ABC�ס�BCD��
���A����CBD����C����BDC����ABC��
�ߡ�ABC����ABD��Ϊ��������Σ�
��BC��BD��
�ߡ�DBC����A+��ABD����C����ABC����DBC+��ABD��
���A����ABD�����A��x�����DBC��x����BDC����C��2x��
��5x��180����
��x��36��
�ʴ�Ϊ��36��
��3����ÿһ�����������ζ�����������Σ���ȷ��
�ڵ��������ε��������������������Σ�����
������������������λ�Ϊ��������Σ���ô�����������ο���ȫ�ȣ���ȷ��
�����һ�����������δ���������ͬ����������Σ���ô������������Ҳһ����Ϊ��������Σ�����
�ʴ�Ϊ�٢ۣ�