题目内容
【题目】如图，抛物线y=（x﹣1）2+n与x轴交于A，B两点（A在B的左侧），与y轴交于点C（0，﹣3），点D与点C关于抛物线的对称轴对称．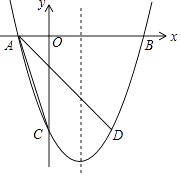
（1）求抛物线的解析式及点D的坐标；
（2）点P是抛物线对称轴上的一动点，当△PAC的周长最小时，求出点P的坐标；
（3）点Q在x轴上，且∠ADQ=∠DAC，请直接写出点Q的坐标．
【答案】
（1）
解：把C（0，﹣3）代入y=（x﹣1）2+n，得，﹣3=（0﹣1）2+n，
解得n=﹣4，
∴抛物线的解析式为y=（x﹣1）2﹣4，
∴抛物线的对称轴为直线x=1，
∵点D与点C关于抛物线的对称轴对称，
∴点D的坐标为（2，﹣3）
（2）
解：连接PA、PC、PD
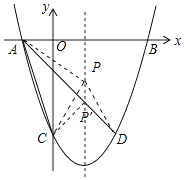
∵点D与点C关于抛物线的对称轴对称
∴PC=PD
∴AC+PA+PC=AC+PA+PD
∵AC为定值，PA+PD≥AD
∴当PA+PC的值最小，即A，P，D三点在同一直线上时△PAC的周长最小，
由y=（x﹣1）2﹣4=0解得，x1=﹣1，x2=3，
∵A在B的左侧，∴A（﹣1，0），
由A，D两点坐标可求得直线AD的解析式为y=﹣x﹣1，
当x=1时，y=﹣x﹣1=﹣2，
∴当△PAC的周长最小时，点P的坐标为（1，﹣2）
（3）
解：如图2中，
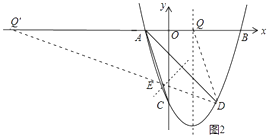
①作DQ∥AC交x轴于点Q，此时∠DQA=∠DAC，满足条件．
∵A（﹣1，0），C（0，﹣3），
∴直线AC的解析式为y=﹣3x﹣3，
∴直线QD的解析式为y=﹣3x+3，
令y=0得x=1，
∴Q（1，0）．
②设线段AD的垂直平分线交AC于E，直线DE与x的交点为Q′，此时∠Q′DA=′CAD，满足条件，
∵直线AD的解析式为y=﹣x﹣1，
∴线段AD的中垂线是解析式为y=x﹣2，
由 
解得 
，
∴E（﹣ 
，﹣ 
），
∴直线DE的解析式为y=﹣ 
x﹣ 
，
令y=0得到x=﹣7，
∴Q′（﹣7，0）．
综上所述，Q点坐标为（1，0）或（﹣7，0）
【解析】（1）利用待定系数法即可求出n，利用对称性C、D关于对称轴对称即可求出点D坐标．（2）A，P，D三点在同一直线上时△PAC的周长最小，求出直线AD的解析式即可解决问题．（3）分两种情形①作DQ∥AC交x轴于点Q，此时∠DQA=∠DAC，满足条件．②设线段AD的垂直平分线交AC于E，直线DE与x的交点为Q′，此时∠Q′DA=′CAD，满足条件，分别求解即可．
【考点精析】根据题目的已知条件，利用二次函数的图象和二次函数的性质的相关知识可以得到问题的答案，需要掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．
