题目内容
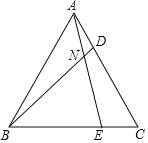
【题目】如图,将两块直角三角形的一条直角边重合叠放,已知AC=BC= ![]() +1,∠D=60°,则两条斜边的交点E到直角边BC的距离是 .
+1,∠D=60°,则两条斜边的交点E到直角边BC的距离是 . 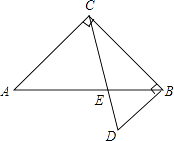
【答案】1
【解析】解:过点E作EH垂直BC于H。

∵∠CBD=90°,∠D=60°,
∴∠BCD=30°,
∴∠ACE=60°,
∵AC=BC= ![]() +1,
+1,
∴BD= ![]() ,AB=
,AB= ![]() (
( ![]() +1),
+1),
∵∠AEC=∠BED,
∴△BDE∽△ACE,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴BE= ![]() ,AE=
,AE= ![]() ,
,
∵∠ACB=90°,
∴△BHE∽△BCA,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴EH=1,
故答案为1.
过点E作EH垂直BC于H。AC=BC=![]() ,∠D=60°,根据特殊锐角的三角函数值可以求出BD,AB的长,进而判断出△BDE∽△ACE,根据相似三角形对应边成比例得出BE,AE的长,再判断出△BHE∽△BCA,根据对应边成比例得出EH的长。
,∠D=60°,根据特殊锐角的三角函数值可以求出BD,AB的长,进而判断出△BDE∽△ACE,根据相似三角形对应边成比例得出BE,AE的长,再判断出△BHE∽△BCA,根据对应边成比例得出EH的长。

练习册系列答案
相关题目
【题目】某服装店用4400元购进A,B两种新式服装,按标价售出后可获得毛利润2800元(毛利润=售价﹣进价),这两种服装的进价,标价如表所示.
类型价格 | A型 | B型 |
进价(元/件) | 60 | 100 |
标价(元/件) | 100 | 160 |
(1)请利用二元一次方程组求这两种服装各购进的件数;
(2)如果A种服装按标价的9折出售,B种服装按标价的8折出售,那么这批服装全部售完后,服装店比按标价出售少收入多少元?