Question

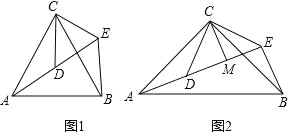
【题目】如图，△ABC是等边三角形，D，E分别是AC，BC上的两点，且AD＝CE，AE，BD相交于点N，则∠DNE的度数是______．

Answer 1

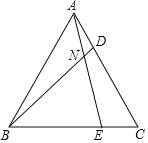
【答案】120°

【解析】

由等边三角形的性质得出AB＝CA，∠BAD＝∠ACE＝60°，由SAS即可证明△ABD≌△CAE，得到∠ABD＝∠CAE，利用外角∠BNE＝∠BAN+∠ABD，即可解决问题．

解：∵△ABC是等边三角形，

∴AB＝CA，∠BAD＝∠ACE＝60°，

在△ABD和△CAE中，

，

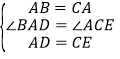∴△ABD≌△CAE（SAS），

∴∠ABD＝∠CAE，

∵∠BNE＝∠BAN+∠ABD，

∴∠BNE＝∠BAN+∠CAE＝∠BAC＝60°，

∴∠DNE＝180°﹣60°＝120°

故答案为:120°．