题目内容
【题目】在平面直角坐标系![]() 中,
中,![]() 、
、![]() 为平面内不重合的两个点,若
为平面内不重合的两个点,若![]() 到
到![]() 、
、![]() 两点的距离相等,则称点
两点的距离相等,则称点![]() 是线段
是线段![]() 的“似中点”.
的“似中点”.
(1)已知![]() ,
,![]() , 在点
, 在点![]() 、
、![]() 、
、![]() 、
、![]() 中,线段
中,线段![]() 的“似中点”是点 .
的“似中点”是点 .
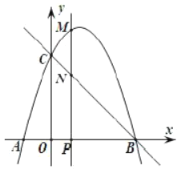
(2)直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
①若点![]() 是线段
是线段![]() 的“似中点”,且在坐标轴.上,求
的“似中点”,且在坐标轴.上,求![]() 点的坐标;
点的坐标;
②若![]() 的半径为2,圆心
的半径为2,圆心![]() 为
为![]() ,若
,若![]() 上存在线段
上存在线段![]() 的“似中点”,请直接写出
的“似中点”,请直接写出![]() 的取值范围.
的取值范围.
【答案】(1)D,F;(2)①(1,0)和(0,![]() );②-3≤t≤5.
);②-3≤t≤5.
【解析】
(1)分别求出点A,B与点C,D,E,F的距离,再根据“似中点”的定义,进行判断即可;
(2)①由题意得:点H为MN的垂直平分线与坐标轴的交点,画出图形,根据含30°角的直角三角形的性质,即可求解;②设点P到H1H2的距离为h,则当h≤2时,![]() 上存在线段
上存在线段![]() 的“似中点”, h=
的“似中点”, h=![]()
![]() ,进而即可求出答案.
,进而即可求出答案.
(1)∵![]() ,
,![]() ,
,![]() 、
、![]() 、
、![]() 、
、![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴![]() ,
,![]() ,
,
∴线段![]() 的“似中点”是点D,F.
的“似中点”是点D,F.
故答案是:D,F;
(2)①由题意可知:M(-1,0),N(0,![]() ),
),
∴∠NMO=60°,MN=![]() ,
,
∵点![]() 是线段
是线段![]() 的“似中点”,且在坐标轴上,
的“似中点”,且在坐标轴上,
∴点H为MN的垂直平分线与坐标轴的交点,
∴∠MH1H2=30°,
∴H1M=2,
∴H1(1,0),
∵OH2=![]() OH1=
OH1=![]() ,
,
∴H2(0,![]() ),
),
综上所述,![]() 点的坐标为:(1,0)和(0,
点的坐标为:(1,0)和(0,![]() );
);
②若![]() 上存在线段
上存在线段![]() 的“似中点”,则
的“似中点”,则![]() 与线段MN的垂直平分线H1H2有公共点.
与线段MN的垂直平分线H1H2有公共点.
设点P到H1H2的距离为h,则当h≤2时,![]() 上存在线段
上存在线段![]() 的“似中点”,
的“似中点”,
∵∠H2H1O=30°,
∴h=![]() H1P=
H1P=![]()
![]() ,
,
∴![]()
![]() ≤2,解得:-3≤t≤5.
≤2,解得:-3≤t≤5.
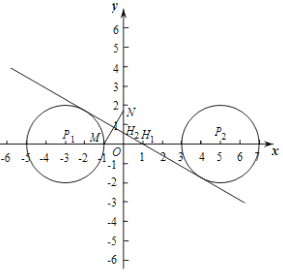

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目