题目内容
【题目】某商场销售一种商品,该商品的进价为每件10元,物价部门限定,每件该商品的销售利润不得超过![]() ,销售过程中发现月销售量
,销售过程中发现月销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间的关系满足:当
(元)之间的关系满足:当![]() 时,月销售量为640件;当
时,月销售量为640件;当![]() 时,销售单价每增加1元,月销售量就减少20件.
时,销售单价每增加1元,月销售量就减少20件.
(1)请直接写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)设该商品的月利润为![]() (元),求
(元),求![]() 与
与![]() 之间的函数关系式,并指出当该商品的销售单价定为多少元时,月利润最大,最大月利润是多少.
之间的函数关系式,并指出当该商品的销售单价定为多少元时,月利润最大,最大月利润是多少.
【答案】(1)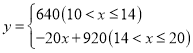 ;(2)
;(2)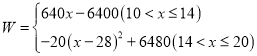 ,当商品的销售单价定为20元时,月利润最大,最大月利润是5200元
,当商品的销售单价定为20元时,月利润最大,最大月利润是5200元
【解析】
(1)根据题意,分当![]() 时和当
时和当![]() 时两种情况即可解答;
时两种情况即可解答;
(2)分两种情况列出W与x的函数关系式,根据一次函数和二次函数的增减性,确定当![]() 时和当
时和当![]() 时的最大值,比较即可解答.
时的最大值,比较即可解答.
解:(1)当![]() 时,y=640,
时,y=640,
当![]() 时,y=640-20(x-14)=-20x+920,
时,y=640-20(x-14)=-20x+920,
∴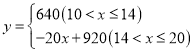
(2)当![]() 时,
时,![]()
当![]() 时,
时,![]()
故![]() 与
与![]() 之间的函数关系式为
之间的函数关系式为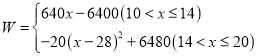
当![]() 时,
时,![]() ,
,
![]() 随
随![]() 的增大而增大,
的增大而增大,
![]() 当
当![]() 时,
时,![]() 取最大值,最大值为2560.
取最大值,最大值为2560.
当![]() 时,
时,![]() ,
,
函数![]() 图象的对称轴为直线
图象的对称轴为直线![]() ,
,
∴在对称轴左侧,![]() 随
随![]() 的增大而增大.当
的增大而增大.当![]() 时,
时,![]() 取最大值,最大值为5200.
取最大值,最大值为5200.
![]() ,当商品的销售单价定为20元时,月利润最大,最大月利润是5200元.
,当商品的销售单价定为20元时,月利润最大,最大月利润是5200元.

练习册系列答案
相关题目