��Ŀ����
����Ŀ���ۺ���ʵ��
�����Ķ� ������ǧ����ǰ���ҹ��ܳ���ѧ���̸߾��������һ��ֱ���۳�һ��ֱ�ǣ���������������ɵ����ģ���ô�Ҿ͵����壬�������������ġ����塱�������������ҹ��Ŵ�������ѧ�����������㾭���У�Ϊ�˷��㣬�ڱ����У����ǰ����ߵı�Ϊ3��4��5�������γ�Ϊ��3��4��5���������Σ����磺���߳��ֱ�Ϊ9��12��15��3![]() ��4
��4![]() ��5
��5![]() �������ξ��ǣ�3��4��5���������Σ��þ���ֽƬ������IJ������������۳��������͵������Σ�
�������ξ��ǣ�3��4��5���������Σ��þ���ֽƬ������IJ������������۳��������͵������Σ�
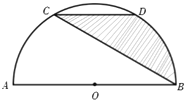
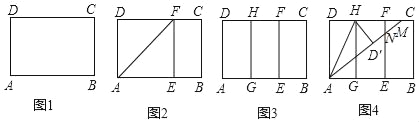
ʵ������ ��ͼ1���ھ���ֽƬABCD�У�AD=8cm��AB=12cm��
��һ������ͼ2����ͼ1�еľ���ֽƬABCD�ع���A��ֱ���۵���ʹ��D����AB�ϵĵ�E�����ۺ�ΪAF������EF�۵���Ȼ���ֽƬչƽ��
�ڶ�������ͼ3����ͼ2�еľ���ֽƬ�ٴ��۵���ʹ��D���F�غϣ��ۺ�ΪGH��Ȼ��չƽ����ȥAF��
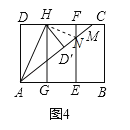
����������ͼ4����ͼ3�еľ���ֽƬ��AH�۵����õ���AD��H������AD���۵����ۺ�ΪAM��AM���ۺ�EF���ڵ�N��Ȼ��չƽ��
������
��1������ͼ2��֤���ı���AEFD�������Σ�
��2������ͼ4���ж�NF��ND���������ϵ��������֤����
��3������ͼ4��֤����AEN��3��4��5���������Σ�
̽������
��4���ڲ�������ĸ������£�ͼ4�л�����Щ�������ǣ�3��4��5���������Σ����ҳ���ֱ��д�����ǵ����ƣ�
���𰸡���1��֤������������2��NF=ND�䣬���ɼ���������3��֤������������4����MFN����MD��H����MDA�ǣ�3��4��5���������Σ�
��������
������1����������������3��4��5���������εĶ���֤�����ɣ�
��2��NF=ND����֤��Rt��HNF��Rt��HND�����ɣ�
��3����������������3��4��5���������εĶ���֤�����ɣ�
��4������AEN�ǣ�3��4��5���������Σ���������AEN���Ƶ������ǣ�3��4��5���������Σ�
����������⣺��1�����ı���ABCD�Ǿ��Σ����D=��DAE=90�������۵�֪��AE=AD����AEF=��D=90�㣬���D=��DAE=��AEF=90�㣬���ı���AEFD�Ǿ��Σ���AE=AD��������AEFD�������Σ�
��2��NF=ND����֤�����£�
����HN�����۵�֪����AD��H=��D=90�㣬HF=HD=HD�䣮
���ı���AEFD�������Σ����EFD=90�㣮
�ߡ�AD��H=90�㣬���HD��N=90�㣮
��Rt��HNF��Rt��HND���У���HN=HN��HF=HD�䣬��Rt��HNF��Rt��HND�䣬��NF=ND�䣮
��3�����ı���AEFD�������Σ���AE=EF=AD=8cm�����۵�֪��AD��=AD=8cm��EN=EF-NF=��8-x���M��
��Rt��AEN�У��ɹ��ɶ����ã�![]() ����
����![]() ����ã�x=2����AN=8+x=10���M����EN=6���M������AN=6��8��10=3��4��5������AEN�ǣ�3��4��5���������Σ�
����ã�x=2����AN=8+x=10���M����EN=6���M������AN=6��8��10=3��4��5������AEN�ǣ�3��4��5���������Σ�
��4��ͼ4�л��С�MFN����MD��H����MDA�ǣ�3��4��5���������Σ�
��CF��AE�����MFN�ס�AEN��
��EN��AE��AN=3��4��5����FN��MF��CN=3��4��5�����MFN�ǣ�3��4��5���������Σ�
ͬ������MD��H����MDA�ǣ�3��4��5���������Σ�

 ���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
���ɿ��õ�Ԫ������ĩר����100��ϵ�д�����Ŀ��2019��3��15�գ��ҹ������ᡱ�����Ļ.13��ʱ������Ը��ص�5000����������ίԱ���ڹ����������ģ�������ҷ�չ��ƣ�ijУ������3��������ʦΪ���˽�ͬѧ�Ƕԡ����ᡱ֪ʶ��֪�������������һ��С���ԣ���������100�֣�����
A��ͬѧ�IJ��Գɼ��ֱ�Ϊ��91 91 86 93 85 89 89 88 87 91
B��ͬѧ�IJ��Գɼ��ֱ�Ϊ��88 97 88 85 86 94 84 83 98 87
�����������ݣ��ش��������⣺
��1������±���
��� | ƽ���� | ��λ�� | ���� | ���� |
A�� | 89 | 89 | b | c |
B�� | 89 | a | 88 | 26.2 |
����a���� ����b���� ����c���� ����
��2������ʦ��B��ͬѧ�IJ��Գɼ��ֳ����鲢���Ƴ���ͼ��ʾƵ���ֲ�ֱ��ͼ�������������벹ȫ��
��3���������Ϸ���������Ϊ�� ���飨�A����B������ͬѧ�Խ��ꡰ���ᡱ֪ʶ��֪���������һЩ����д���������жϵ����ɣ�����д������������ ������ ����