题目内容
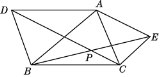
【题目】如图,菱形ABCD对角线交于点O,BE∥AC,AE∥BD,EO与AB交于点F.
(1)试判断四边形AEBO的形状,并说明你的理由;
(2)求证:EO=DC.

【答案】证明见解析
【解析】
(1)由菱形的性质可证明∠BOA=90°,然后再证明四边形AEBO为平行四边形,从而可证明四边形AEBO是矩形;
(2)依据矩形的性质可得到EO=BA,然后依据菱形的性质可得到AB=CD.
(1)四边形AEBO是矩形.
证明:∵BE∥AC,AE∥BD,
∴四边形AEBO是平行四边形.
又∵菱形ABCD对角线交于点O,
∴AC⊥BD,即∠AOB=90°.
∴四边形AEBO是矩形.
(2)∵四边形AEBO是矩形,
∴EO=AB,
在菱形ABCD中,AB=DC.
∴EO=DC.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
【题目】某校要从甲、乙、丙、丁四名学生中选一名参加“汉字听写”大赛,选拔中每名学生的平均成绩 ![]() 及其方差s2如表所示,如果要选拔一名成绩高且发挥稳定的学生参赛,则应选择的学生是( )
及其方差s2如表所示,如果要选拔一名成绩高且发挥稳定的学生参赛,则应选择的学生是( )
甲 | 乙 | 丙 | 丁 | |
| 8.9 | 9.5 | 9.5 | 8.9 |
s2 | 0.92 | 0.92 | 1.01 | 1.03 |
A.甲
B.乙
C.丙
D.丁