Question

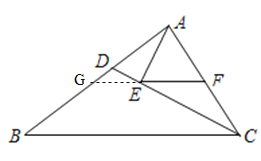
【题目】如图,CD是△ABC的角平分线,AE⊥CD于E,F是AC的中点,

（1）求证:EF∥BC；

（2）猜想：∠B、∠DAE、∠EAC三个角之间的关系，并加以证明.

Answer 1

【答案】（1）证明见解析；

（2）∠EAC=∠B+∠DAE，证明见解析.

【解析】解：（1）∵AE⊥CD于E，F是AC的中点

∴FE=FC

∴∠FEC=∠FCE

∵CD是△ABC的角平分线

∴∠ECB=∠FCE

∴∠ECB=∠FEC

∴EF∥BC ．

（2）∠EAC=∠B+∠DAE．

延长FE交AD于点G；

∵EF∥BC，∴∠DGE=∠B，

∴∠DAE+∠B=∠DAE+∠G=∠AEF．

∵∠AEC=90°，F是斜边AC的中点，∴AF=EF，∴∠EAC=∠AEF．

∴∠EAC=∠B+∠DAE．