ЬтФПФкШн
ЁОЬтФПЁПЪ§бЇаЫШЄЛюЖЏПЮЩЯЃЌаЁжТНЋЕШбќ![]() ЕФЕзБп
ЕФЕзБп![]() гыжБЯп
гыжБЯп![]() жиКЯЃЎ
жиКЯЃЎ
ЃЈ1ЃЉШчЭМ![]() ЃЌдк
ЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌЕу
ЃЌЕу![]() дкБп
дкБп![]() ЫљдкЕФжБЯп
ЫљдкЕФжБЯп![]() ЩЯвЦЖЏЃЌИљОнЁАжБЯпЭтвЛЕуЕНжБЯпЩЯЫљгаЕуЕФСЌЯпжаДЙЯпЖЮзюЖЬЁБЃЌаЁжТЗЂЯж
ЩЯвЦЖЏЃЌИљОнЁАжБЯпЭтвЛЕуЕНжБЯпЩЯЫљгаЕуЕФСЌЯпжаДЙЯпЖЮзюЖЬЁБЃЌаЁжТЗЂЯж![]() ЕФзюаЁжЕЪЧ____________ЃЎ
ЕФзюаЁжЕЪЧ____________ЃЎ
ЃЈ2ЃЉЮЊНјвЛВНдЫгУИУНсТлЃЌдкЃЈ1ЃЉЕФЬѕМўЯТЃЌаЁжТЗЂЯжЃЌЕБ![]() зюЖЬЪБЃЌШчЭМ
зюЖЬЪБЃЌШчЭМ![]() ЃЌдк
ЃЌдк![]() жаЃЌзї
жаЃЌзї![]() ЦНЗж
ЦНЗж![]() НЛ
НЛ![]() гкЕу
гкЕу![]() Еу
Еу![]() ЗжБ№ЪЧБп
ЗжБ№ЪЧБп![]() ЩЯЕФЖЏЕуЃЌСЌНс
ЩЯЕФЖЏЕуЃЌСЌНс![]() аЁжТГЂЪдЬНЫї
аЁжТГЂЪдЬНЫї![]() ЕФзюаЁжЕЃЌаЁжТдк
ЕФзюаЁжЕЃЌаЁжТдк![]() ЩЯНиШЁ
ЩЯНиШЁ![]() ЪЙЕУ
ЪЙЕУ![]() СЌНс
СЌНс![]() взжЄ
взжЄ![]() ЃЌДгЖјНЋ
ЃЌДгЖјНЋ![]() зЊЛЏЮЊ
зЊЛЏЮЊ![]() зЊЛЏЕНЃЈ1ЃЉЕФЧщПіЃЌдђ
зЊЛЏЕНЃЈ1ЃЉЕФЧщПіЃЌдђ![]() ЕФзюаЁжЕЮЊЁЁЁЁЁЁЁЁЃЛ
ЕФзюаЁжЕЮЊЁЁЁЁЁЁЁЁЃЛ
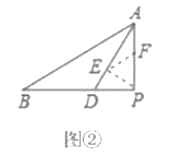
ЃЈ3ЃЉНтОіЮЪЬтЃКШчЭМ![]() ЃЌдк
ЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЪЧБп
ЪЧБп![]() ЩЯЕФЖЏЕуЃЌСЌНс
ЩЯЕФЖЏЕуЃЌСЌНс![]() НЋЯпЖЮ
НЋЯпЖЮ![]() ШЦЕу
ШЦЕу![]() ЫГЪБеыа§зЊ
ЫГЪБеыа§зЊ![]() ЃЌЕУЕНЯпЖЮ
ЃЌЕУЕНЯпЖЮ![]() СЌНс
СЌНс![]() ЃЌЧѓЯпЖЮ
ЃЌЧѓЯпЖЮ![]() ЕФзюаЁжЕЃЎ
ЕФзюаЁжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉ2ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ3ЃЎ
ЃЛЃЈ3ЃЉ3ЃЎ
ЁОНтЮіЁП
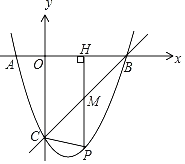
ЃЈ1ЃЉИљОнЕШбќШ§НЧаЮЕФаджЪЧѓНтМДПЩЃЛ
ЃЈ2ЃЉИљОнаЁжТЕФЫМТЗЃЌАбНЋ![]() зЊЛЏЮЊ
зЊЛЏЮЊ![]() МДPЃЌEЃЌNШ§ЕуЙВЯпЧв
МДPЃЌEЃЌNШ§ЕуЙВЯпЧв![]() ЪБ
ЪБ![]() ЕФжЕзюаЁЃЛ
ЕФжЕзюаЁЃЛ
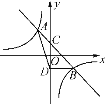
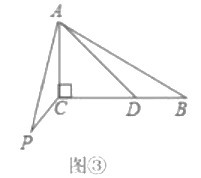
ЃЈ3ЃЉдк![]() ЩЯШЁвЛЕу
ЩЯШЁвЛЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЎгЩ
ЃЎгЩ![]() ЃЌЭЦГі
ЃЌЭЦГі![]() ЃЌвзжЊ
ЃЌвзжЊ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФжЕзюаЁЃЌЧѓГі
ЕФжЕзюаЁЃЌЧѓГі![]() ЕФзюаЁжЕМДПЩНтОіЮЪЬтЃЎ
ЕФзюаЁжЕМДПЩНтОіЮЪЬтЃЎ
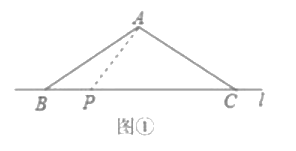
ЃЈ1ЃЉШчЭМЃЌЙ§ЕуAзї![]() ЃЌДЫЪБAPЕФжЕзюаЁЃЎ
ЃЌДЫЪБAPЕФжЕзюаЁЃЎ
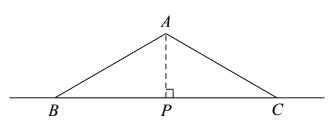
Ёп![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
ЙЪД№АИЮЊЃК2ЃЎ
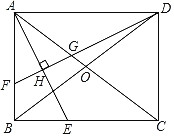
ЃЈ2ЃЉИљОнаЁжТЕФЫМТЗзїГіЭМаЮЃЌПЩжЊЕБ![]() ЪБ
ЪБ![]() ЕФжЕзюаЁЃЌШчЭМЃК
ЕФжЕзюаЁЃЌШчЭМЃК
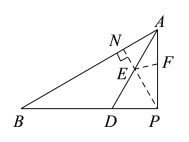
Ёп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЙЪД№АИЮЊЃК![]() ЃЎ
ЃЎ
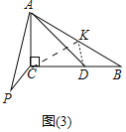
ЃЈ3ЃЉШчЭМ3жаЃЌдк![]() ЩЯШЁвЛЕу
ЩЯШЁвЛЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЪБЃЌ
ЪБЃЌ![]() ЕФжЕзюаЁЃЌзюаЁжЕЮЊ3ЃЌ
ЕФжЕзюаЁЃЌзюаЁжЕЮЊ3ЃЌ
![]() ЕФзюаЁжЕЮЊ3ЃЎ
ЕФзюаЁжЕЮЊ3ЃЎ

 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ