题目内容
【题目】如图,已知![]() 是⊙
是⊙![]() 的直径,
的直径,![]() ,
,![]() 和
和![]() 是圆
是圆![]() 的两条切线,
的两条切线,![]() ,
,![]() 为切点,过圆上一点
为切点,过圆上一点![]() 作⊙
作⊙![]() 的切线
的切线![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,连接
,连接![]() ,
,![]() .若
.若![]() ,则
,则![]() 等于( )
等于( )

A. 0.5 B. 1
C. ![]() D.
D. ![]()
【答案】C
【解析】
连接OM、OC,根据圆周角定理可得∠AOC=2∠ABC=60°,由切线长定理可得MA=MC且∠MAO=∠MCO=90°,利用HL证明Rt△AOM≌Rt△COM,即可得∠AOM=∠COM=![]() ∠AOC=30°,在Rt△AOM中求得AM的长即可.
∠AOC=30°,在Rt△AOM中求得AM的长即可.
连接OM,OC,
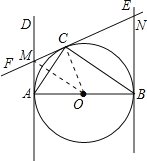
∵∠ABC=30°,
∴∠AOC=2∠ABC=60°,
∵MA,MC分别为⊙O的切线,
∴MA=MC,且∠MAO=∠MCO=90°,
在Rt△AOM和Rt△COM中,
MA=MC,OM=OM,
∴Rt△AOM≌Rt△COM(HL),
∴∠AOM=∠COM=![]() ∠AOC=30°,
∠AOC=30°,
在Rt△AOM中,OA=![]() AB=1,∠AOM=30°,
AB=1,∠AOM=30°,
∴tan30°=![]() ,即
,即![]() ,
,
解得:AM=![]() .
.
故答案为:![]() .
.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目






