��Ŀ����
����Ŀ����ͼ���������ϵ�A��ʾ��a����C��ʾ��c����|a+10|+��c��20��2��0�����ǰ�����������֮��ľ����ñ�ʾ����Ĵ�д��ĸһ���ǣ����磬��A���B֮��ľ������AB��
![]()
��1����a��c��ֵ��
��2����֪��DΪ������һ���㣬������CD+AD��32��ֱ��д����D��ʾ������
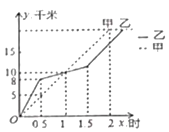
��3������B����1��Ӧ�ĵ㿪ʼ�����˶����ٶ�Ϊÿ��1����λ���ȣ�ͬʱ��A��C���������˶�����A��C���ٶȷֱ�Ϊÿ��3����λ���ȡ�ÿ��4����λ���ȣ��˶�ʱ��Ϊt�룺
������A�����˶�����C�����˶���AB��BC����t��ֵ��
������A�����˶�����C�����˶���2AB��m��BC��ֵ����ʱ��t�ı仯���ı䣬�����m��ֵ��
���𰸡���1��a����10��c��20����2��D���ʾ����Ϊ��11��21����3������t��![]() ��
��![]() ����m��
����m��![]()
��������
��1�����÷Ǹ��������ʵ�a+10=0��c-20=0�����a��c��ֵ���ɣ�
��2���ֵ�D�ڵ�A����࣬��A��C֮�䣬�ڵ�D���Ҳ���������ֱ�������⼴�ɣ�
��3�������������ʾ��A��B��C�����˶�t����ʾ����������AB=BC�ɵù���t�ķ��̣��ⷽ�̼�����ô𰸣�
�����������ʾ��A��B��C�����˶�t����ʾ��������ʾ��AB��BC�ij����̶�����2AB��m��BC �ɵù���t�Ĵ���ʽ����������2AB��m��BC��ֵ����ʱ��t�ı仯���ı伴����ô�.
��1����|a+10|+��c��20��2��0��
��a+10=0��c-20=0��
��a����10��c��20��
��2���ߵ�A��ʾ��-10����C��ʾ��20��
��AC=30��
����D�ڵ�A����࣬
![]()
��CD+AD��32��
��AD+AC+AD��32��
��AD��1��
����D���ʾ����Ϊ��10��1����11��
����D�ڵ�A��C֮��ʱ��
![]()
��CD+AD��AC��30��32��
�������ڵ�D��ʹCD+AD��32��
����D�ڵ�C���Ҳ�ʱ��
![]()
��CD+AD��32��
��AC+CD+CD��32��
��CD��1��
����D���ʾ����Ϊ20+1��21��
����������D���ʾ����Ϊ��11��21��
��3�����������֪��A�˶�t����ʾ����Ϊ-10+3t����B�˶�t����ʾ����Ϊ1+t����C�˶�t����ʾ����Ϊ20-4t��
��AB��BC��
��|��1+t��������10+3t��|��|��1+t������20��4t��|
��t��![]() ��
��![]() ��
��
���������֪��A�˶�t����ʾ����Ϊ-10-3t����B�˶�t����ʾ����Ϊ1+t����C�˶�t����ʾ����Ϊ20+4t��
��AB=1+t-(-10-3t)=11+4t��BC=20+4t-(1+t)=19+3t��
��2AB��m��BC��2����11+4t����m��19+3t������8��3m��t+22��19m��
�֡�2AB��m��BC��ֵ����ʱ��t�ı仯���ı䣬
��8��3m��0��
��m��![]() .
.

 â���̸������Ծ�ϵ�д�
â���̸������Ծ�ϵ�д�����Ŀ���Ķ����в��ϣ�
������һ�����⣺����x ��һԪ���η���a x2+bx+c=0��a��0������������ȵ��ҷ����ʵ������̽��a��b��c�����������
С������ѧϰ�����ľ��飬��Ϊ���ԴӶ��κ����ĽǶȿ�һԪ���η��̣�������С����̽�����̣�
����һԪ���η���ax2+bx+c=0��a��0����Ӧ�Ķ��κ���Ϊy=ax2+bx+c��a��0����
�ڽ������κ���ͼ���Եõ���Ӧ��һԪ������a��b��c������������б����£�
���̸��ļ������壺�뽫��2����������
������������� | ��Ӧ�Ķ��κ����Ĵ���ͼ�� | a��b��c��������� |
���������� ����ȵĸ�ʵ�� |
|
|
_____ |
|
|
���������� ����ȵ���ʵ�� | _____ | _____ |
��1���ο�С��������������������������
��2����һԪ���η���mx2����2m+3��x��4m=0��һ����ʵ����һ����ʵ�����Ҹ�ʵ�����ک�1����ʵ��m��ȡֵ��Χ��