题目内容
【题目】把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=4 cm,求球的半径长.
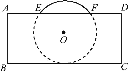
【答案】球的半径长为2.5 cm.
【解析】
取EF的中点M，作MN⊥AD交BC于点N，则MN经过球心O，连接OF，设OF＝
，则OM＝4，MF＝2，然后在Rt△MOF中利用勾股定理求得OF的长即可．
解:如图,取EF的中点M,作MN⊥AD交BC于点N,则MN经过球心O,连接OF.
∵四边形ABCD是矩形,∴∠C=∠D=90°,
∴四边形CDMN是矩形,∴MN=CD=4,
设OF=x,则ON=OF,
∴OM=MN-ON=4-x,MF=2,
在Rt△OMF中,OM2+MF2=OF2,
即(4-x)2+22=x2,解得x=2.5.
答:球的半径长为2.5 cm.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】.某酒厂生产A，B两种品牌的酒，平均每天两种酒共可售出600瓶，每种酒每瓶的成本和售价如表所示，设平均每天共获利y元，平均每天售出A种品牌的酒x瓶.
A | B | |
成本（元） | 50 | 35 |
售价（元） | 70 | 50 |
（1）请写出y关于x的函数关系式；
（2）如果该厂每天至少投入成本25000元，且售出的B种品牌的酒不少于全天销售总量的55%，那么共有几种销售方案?并求出每天至少获利多少元?
