题目内容
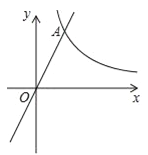
【题目】如图1,在平面直角坐标系中,抛物线y=x2-4x-5与x轴分别交于A、B(A在B的左边),与y轴交于点C,直线AP与y轴正半轴交于点M,交抛物线于点P,直线AQ与y轴负半轴交于点N,交抛物线于点Q,且OM=ON,过P、Q作直线l
(1) 探究与猜想:
① 取点M(0,1),直接写出直线l的解析式
取点M(0,2),直接写出直线l的解析式
② 猜想:
我们猜想直线l的解析式y=kx+b中,k总为定值,定值k为__________,请取M的纵坐标为n,验证你的猜想
(2) 如图2,连接BP、BQ.若△ABP的面积等于△ABQ的面积的3倍,试求出直线l的解析式

【答案】(1)①PQ:y=6x-29,PQ:y=6x-26;
(2)k=6;
(3)直线PQ的解析式为y=6x-21
【解析】试题分析:(1)、①、首先根据二次函数解析式得出点A的坐标,然后根据待定系数法求出直线l的解析式;②、设设M(0,n),然后分别求出直线AP和AQ的解析式,然后根据直线与抛物线的交点求出点P和点Q的坐标,从而得出直线PQ的解析式,得出k的值;(2)、根据三角形的面积关系得出点P的坐标,从而得出直线PQ的函数解析式.
试题解析:(1) ① P(6,7)、Q(4,-5),PQ:y=6x-29
② 设M(0,n) AP的解析式为y=nx+n AQ的解析式为y=-nx-n
联立![]() ,整理得x2-(4+n)x-(5+n)=0
,整理得x2-(4+n)x-(5+n)=0
∴xA+xP=-1+xP=4+n,xP=5+n 同理:xQ=5-n
设直线PQ的解析式为y=kx+b
联立![]() ,整理得x2-(4+k)x-(5+b)=0 ∴xP+xQ=4+k
,整理得x2-(4+k)x-(5+b)=0 ∴xP+xQ=4+k
∴5+n+5-n=4+k,k=6
(3) ∵S△ABP=3S△ABQ ∴yP=-3yQ ∴kxP+b=-3(kxQ+b) ∵k=6 ∴6xP+18xQ=-b
∴6(5+n)+18(5-n)=4b,解得b=3n-30
∵xP·xQ=-(5+b)=-5-3n+30=(5+n)(5-n),解得n=3 ∴P(8,27)
∴直线PQ的解析式为y=6x-21

【题目】二次函数图象上部分点的坐标满足下表:则该函数图象的顶点坐标为( )
x | … | -3 | -2 | -1 | 0 | 1 | … |
y | … | -3 | -2 | -3 | -6 | -11 | … |
A. (-3,-3)B. (-2,-2)C. (-1,-3)D. (0,-6)