Question

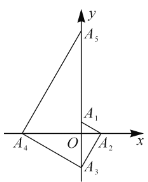
【题目】如图，已致点的坐标为，点在轴的正半轴上，且．过点作，交轴于点；过点作，交轴于点；过点作，交轴于点；……；按此规律进行下去，则点的坐标为（ ）

A.B.C.D.

Answer 1

【答案】C

【解析】

通过解直角三角形可得出点A2的坐标，同理可得出点A3，A4，A5，A6，A7，…的坐标，根据坐标的变化可得出变化规律“点A4n+1的坐标为（0，32n）（n为正整数）”，再结合2021=505×4+1即可得出点A2021的坐标，此题得解．

∵∠A1A2O=30°，OA1=1，
∴OA2=，
∴点A2的坐标为（，0），
同理，A3（0，-3，），A4（-3，0），A5（0，9），A6（9，0），A7（0，-27），…，
∴点A4n+1的坐标为（0，32n）（n为正整数）．
∵2021=505×4+1，
∴点A2021的坐标为（0，31010）．
故选：C．