题目内容
【题目】两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图,点![]() ,
,![]() ,
,![]() 在同一条直线上,连结DC
在同一条直线上,连结DC

(1)请判断![]() 与
与![]() 的位置关系,并证明
的位置关系,并证明
(2)若![]() ,
,![]() ,求
,求![]() 的面积
的面积
【答案】(1)DC⊥BE,见解析;(2)6
【解析】
(1)根据等腰直角三角形的性质可以得出△ABE≌△ACD,得出∠AEB=∠ADC,进而得出∠AEC=90°,就可以得出结论;
(2)根据三角形的面积公式即可得到结论.
(1)证明: ∵△ABC和△ADE是等腰直角三角形
∴AB=AC,AE=AD,∠BAC=∠EAD=90°
∴∠BAC+∠EAC=∠DAE+∠EAC
∴∠BAE=∠CAD
在△ABE和△ACD中
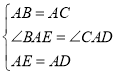
∴△ABE≌△ACD(SAS)
∴∠AEB=∠ADC
∵∠ADC+∠AFD=90°
∴∠AEB+∠AFD=90°
∵∠AFD=∠CFE
∴∠AEB+∠CFE=90°
∴∠FCE=90°
∴DC⊥BE
(2)解:∵CE=2,BC=4
∴BE=6
∵△ABE≌△ACD
∴CD=BE=6
∴![]() .
.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
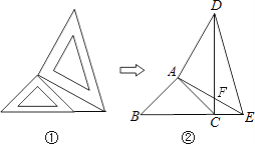
【题目】如图,在平面直角坐标系中,直线y1=2x﹣2与双曲线y2=![]() 交于A、C两点,AB⊥OA交x轴于点B,且OA=AB.
交于A、C两点,AB⊥OA交x轴于点B,且OA=AB.
(1)求双曲线的解析式;
(2)求点C的坐标,并直接写出y1<y2时x的取值范围.
【题目】某校八年级数学课外兴趣小组的同学积极参加义工活动,小庆对全体小组成员参加活动次数的情况进行统计解析,绘制了如下不完整的统计表和统计图(图).
次数 | 10 | 8 | 6 | 5 |
人数 | 3 | a | 2 | 1 |
(1)表中a= ;
(2)请将条形统计图补充完整;
(3)从小组成员中任选一人向学校汇报义工活动情况,参加了10次活动的成员被选中的概率有多少?