Question

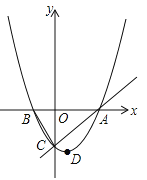
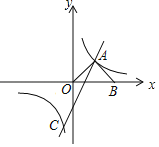
【题目】如图，在平面直角坐标系中，直线y1=2x﹣2与双曲线y2=交于A、C两点，AB⊥OA交x轴于点B，且OA=AB．

（1）求双曲线的解析式；

（2）求点C的坐标，并直接写出y1＜y2时x的取值范围．

Answer 1

【答案】（1）；（2）C（﹣1，﹣4），x的取值范围是x＜﹣1或0＜x＜2．

【解析】（1）作高线AC，根据等腰直角三角形的性质和点A的坐标的特点得：x=2x﹣2，可得A的坐标，从而得双曲线的解析式；

（2）联立一次函数和反比例函数解析式得方程组，解方程组可得点C的坐标，根据图象可得结论．

（1）∵点A在直线y1=2x﹣2上，

∴设A（x，2x﹣2），

过A作AC⊥OB于C，

∵AB⊥OA，且OA=AB，

∴OC=BC，

∴AC=OB=OC，

∴x=2x﹣2，

x=2，

∴A（2，2），

∴k=2×2=4，

∴；

（2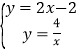）∵，解得：，，

∴C（﹣1，﹣4），

由图象得：y1＜y2时x的取值范围是x＜﹣1或0＜x＜2．