题目内容
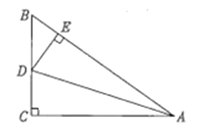
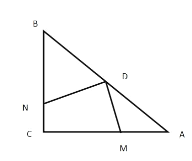
【题目】如图,![]() 是边长为9的等边三角形,
是边长为9的等边三角形,![]() 是
是![]() 边上一动点,由
边上一动点,由![]() 向
向![]() 运动(与
运动(与![]() 、
、![]() 不重合),
不重合),![]() 是
是![]() 延长线上一动点,与点
延长线上一动点,与点![]() 同时以相同的速度由
同时以相同的速度由![]() 向
向![]() 延长线方向运动(
延长线方向运动(![]() 不与
不与![]() 重合),过
重合),过![]() 作
作![]() 于
于![]() ,连接
,连接![]() 交
交![]() 于
于![]()

(1)若![]() 时,求
时,求![]() 的长
的长
(2)当点![]() ,
,![]() 运动时,线段
运动时,线段![]() 与线段
与线段![]() 是否相等?请说明理由
是否相等?请说明理由
(3)在运动过程中线段![]() 的长是否发生变化?如果不变,求出线段
的长是否发生变化?如果不变,求出线段![]() 的长;如果发生变化,请说明理由
的长;如果发生变化,请说明理由
【答案】(1)当∠BQD=30° 时,AP=3;(2)相等,见解析;(3)DE的长不变,![]()
【解析】
(1)先判断出∠QPC是直角,再利用含30°的直角三角形的性质得出QC=2PC,建立方程求解决即可;
(2)先作出PF∥BC得出∠PFA=∠FPA=∠A=60°,进而判断出△DBQ≌△DFP得出DQ=DP即可得出结论;
(3)利用等边三角形的性质得出EF=![]() AF,借助DF=DB,即可得出DF=
AF,借助DF=DB,即可得出DF=![]() BF,最后用等量代换即可.
BF,最后用等量代换即可.
(1)解:∵△ABC是边长为9的等边三角形
∴∠ACB=60°,且∠BQD=30°
∴∠QPC=90°
设AP=![]() ,则PC=
,则PC=![]() ,QB=
,QB=![]()
∴QC=![]()
∵在Rt△QCP中,∠BQD=30°
∴PC=![]() QC 即
QC 即![]()
解得![]()
∴ 当∠BQD=30° 时,AP=3
(2)相等,
证明:过P作PF∥QC,则△AFP是等边三角形
∴AP=PF,∠DQB=∠DPF
∵P、Q同时出发,速度相同,即BQ=AP,
∴BQ=PF,
在△DBQ和△DFP中,
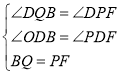
∴△DBQ≌△DFP(AAS)
∴QD=PD
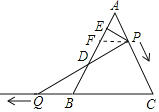
(3)解:不变,
由(2)知△DBQ≌△DFP
∴BD=DF
∵△AFP是等边三角形,PE⊥AB,
∴AE=EF,
∴DE=DF+EF=![]() BF+
BF+![]() FA=
FA=![]() AB=
AB=![]() 为定值,即DE的长不变.
为定值,即DE的长不变.

【题目】中央电视台的“朗读者”节目激发了同学们的读书热情,为了引导学生“多读书,读好书“,某校对八年级部分学生的课外阅读量进行了随机调查,整理调查结果发现,学生课外阅读的本书最少的有5本,最多的有8本,并根据调查结果绘制了不完整的图表,如图所示:
本数(本) | 频数(人数) | 频率 |
5 | a | 0.2 |
6 | 18 | 0.36 |
7 | 14 | b |
8 | 8 | 0.16 |
合计 | 50 | c |
我们定义频率=![]() ,比如由表中我们可以知道在这次随机调查中抽样人数为50人课外阅读量为6本的同学为18人,因此这个人数对应的频率就是
,比如由表中我们可以知道在这次随机调查中抽样人数为50人课外阅读量为6本的同学为18人,因此这个人数对应的频率就是![]() =0.36.
=0.36.
(1)统计表中的a、b、c的值;
(2)请将频数分布表直方图补充完整;
(3)求所有被调查学生课外阅读的平均本数;
(4)若该校八年级共有600名学生,你认为根据以上调查结果可以估算分析该校八年级学生课外阅读量为7本和8本的总人数为多少吗?请写出你的计算过程.