题目内容
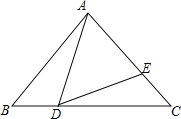
【题目】如图,在![]() 中,∠BAC=90°,AB=AC=2,点
中,∠BAC=90°,AB=AC=2,点![]() 分别在
分别在![]() 上(点
上(点![]() 不与点
不与点![]() 重合),且
重合),且![]() 45°,若
45°,若![]() 是等腰三角形,则
是等腰三角形,则![]() ______.
______.
【答案】![]() 或
或![]()
【解析】
由题意可知D与B、C不重合,所以分两种情况讨论:①当AD=BD,此时可得出∠B=∠BAD=45°,从而得出△ADB为等腰直角三角形,从而△ACD也为等腰直角三角形,进而求而DE的长;②当AB=BD,可得BD,CD的长,再根据等角对等边得出CE=CD,进而可得AE的长.
解:∵AB=AC,∠BAC=90°,∴∠B=∠C=45°.
由题意点D不与点B,C重合,分以下两种情况:
①当AD=BD时(如图1),
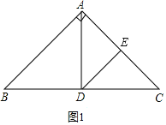
∴∠B=∠BAD=45°,∴∠ADB =90°=∠ADC,
又AB=AC,∴AD平分∠BAC,∴D为BC的中点,
∴AD=CD,
又∠ADE=45°,
∴∠ADE=∠CDE=45°,即DE平分∠ADC,
∴E为AC边的中点,
∴CE=AE=1;
②当AB=BD时(如图2),
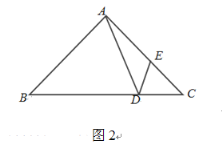
∵∠B=45°,∴∠BAD=∠BDA=67.5°.
∵∠ADE=45°,∴∠CDE=180°-∠BDA-∠ADE=67.5°,
∴∠CED=180°-∠C-∠CDE=67.5°,
∴CD=CE.
∵AB=AC=2,∠BAC=90°,∴BC=2![]() ,
,
∴CD=BC-BD=BC-AB=2![]() -2,
-2,
∴CE=2![]() -2,
-2,
∴AE=AC-CE=2-(2![]() -2)=4-2
-2)=4-2![]() .
.
综上所述,CE的长为1或4-2![]() .
.
故答案为:1或4-2![]() .
.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目