ЬтФПФкШн
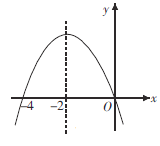
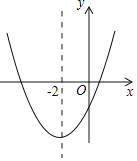
ЁОЬтФПЁПЖўДЮКЏЪ§yЃНax2+bx+cЃЈaЁй0ЃЉЕФДѓжТЭМЯѓШчЭМЫљЪОЃЌЖЅЕузјБъЮЊЃЈЉ2ЃЌЉ9aЃЉЃЌЯТСаНсТлЃКЂйabcЃМ0ЃЛЂк4a+2b+cЃО0ЃЛЂл5aЉb+cЃН0ЃЛЂмШєЗНГЬaЃЈx+5ЃЉЃЈxЉ1ЃЉЃНЉ1гаСНИіИљx1КЭx2ЃЌЧвx1ЃМx2ЃЌдђЉ5ЃМx1ЃМx2ЃМ1ЃЛЂнШєЗНГЬ|ax2+bx+c|ЃН1гаЫФИіИљЃЌдђетЫФИіИљЕФКЭЮЊЉ8ЃЌЦфжае§ШЗЕФНсТлгаЃЈЁЁЁЁЃЉ
A.ЂйЂкЂлЂмB.ЂйЂкЂлЂнC.ЂкЂлЂмЂнD.ЂйЂкЂмЂн
ЁОД№АИЁПD
ЁОНтЮіЁП
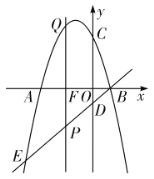
ИљОнПЊПкЗНЯђЁЂЖдГЦжсЁЂгыyжсЕФНЛЕуПЩХаЖЯЂйЃЛИљОнЖЅЕузјБъЮЊЃЈЉ2ЃЌЉ9aЃЉЃЌЧѓГіbЁЂcгыaЕФЙиЯЕЃЌПЩХаЖЯЂкКЭЂлЃЛЯШЧѓГіХзЮяЯпгыxжсЕФНЛЕуЃЌПЩХаЖЯЂмЃЛИљОнИљгыЯЕЪ§ЕФЙиЯЕПЩХаЖЯЂнЃЎ
НтЃКЁпХзЮяЯпЕФПЊПкЯђЩЯЃЌдђaЃО0ЃЌЖдГЦжсдкyжсЕФзѓВрЃЌдђbЃО0ЃЌНЛyжсЕФИКАыжсЃЌдђcЃМ0ЃЌ
ЁрabcЃМ0ЃЌЫљвдЂйНсТле§ШЗЃЛ
ЁпХзЮяЯпЕФЖЅЕузјБъ(-2ЃЌ-9a)ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёрb=4aЃЌc=-5aЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊy=ax2+4ax-5aЃЌ
Ёр4a+2b+c=4a+8a-5a=7aЃО0ЃЌЫљвдЂкНсТле§ШЗЃЌ
5a-b+c=5a-4a-5a=-4aЃМ0ЃЌЙЪЂлНсТле§ШЗЃЌ
ЖдгкЗНГЬax2+4ax-5a=0ЃЌ
ЁпaЃО0ЃЌ
Ёрx2+4x-5=0ЃЌ
НтЕУx1=-5ЃЌx2=1ЃЌ
ЁрХзЮяЯпy=ax2+4ax-5aНЛxжсгк(-5ЃЌ0)ЃЌ(1ЃЌ0)ЃЌ
ЁрШєЗНГЬa(x+5)(x-1)=-1гаСНИіИљx1КЭx2ЃЌЧвx1ЃМx2ЃЌдђ-5ЃМx1ЃМx2ЃМ1ЃЌЙЪНсТлЂме§ШЗЃЌ
ШєЗНГЬ|ax2+bx+c|=1гаЫФИіИљЃЌЩшЗНГЬax2+bx+c=1ЕФСНИљЗжБ№ЮЊx1ЃЌx2ЃЌдђ![]() ЃЌПЩЕУx1+x2=-4ЃЌЩшЗНГЬax2+bx+c=-1ЕФСНИљЗжБ№ЮЊx3ЃЌx4ЃЌдђ
ЃЌПЩЕУx1+x2=-4ЃЌЩшЗНГЬax2+bx+c=-1ЕФСНИљЗжБ№ЮЊx3ЃЌx4ЃЌдђ![]() ЃЌПЩЕУx3+x4=-4ЃЌЫљвдетЫФИіИљЕФКЭЮЊ-8ЃЌЙЪНсТлЂне§ШЗЃЎ
ЃЌПЩЕУx3+x4=-4ЃЌЫљвдетЫФИіИљЕФКЭЮЊ-8ЃЌЙЪНсТлЂне§ШЗЃЎ
ЙЪбЁЃКDЃЎ