题目内容
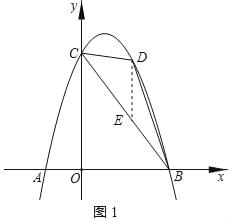
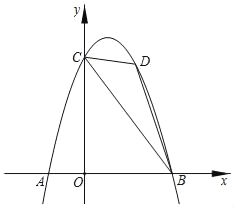
【题目】如图，抛物线y=ax2+bx+6经过点A（﹣2，0），B（4，0）两点，与y轴交于点C，点D是抛物线上一个动点，设点D的横坐标为m（1＜m＜4）连接BC，DB，DC．
（1）求抛物线的函数解析式；
（2）△BCD的面积是否存在最大值，若存在，求此时点D的坐标；若不存在，说明理由；
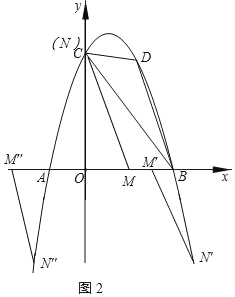
（3）在（2）的条件下，若点M是x轴上一动点，点N是抛物线上一动点，试判断是否存在这样的点M，使得以点B，D，M，N为顶点的四边形是平行四边形．若存在，请直接写出点M的坐标；若不存在，请说明理由．
【答案】（1）
；（2）存在，D的坐标为（2，6）；（3）存在这样的点M，使得以点B，D，M，N为顶点的四边形是平行四边形，点M的坐标为：（2，0）或（6，0）或（
，0）或（
，0）．
【解析】
（1）根据点
，利用待定系数法求解即可；
（2）先根据函数解析式求出点C、D坐标，再将过点D作y轴的平行线交BC于点E，利用待定系数法求出直线BC的函数解析式，从而得出点E坐标，然后根据
得出
的面积表达式，最后利用二次函数的性质求出的面积取最大值时m的值，从而可得点D坐标；
（3）根据平行四边形的定义分两种情况：BD为平行四边形的边和BD为平行四边形的对角线，然后先分别根据平行四边形的性质求出点N坐标，从而即可求出点M坐标．
（1）∵抛物线
经过点
∴
解得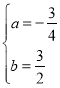
故抛物线的解析式为；
（2）的面积存在最大值．求解过程如下：
，当
时，
由题意，设点D坐标为
，其中
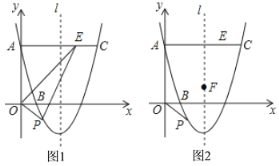
如图1，过点D作y轴的平行线交BC于点E
设直线BC的解析式为
把点
代入得
解得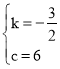
∴直线BC的解析式为
∴可设点E的坐标为
由二次函数的性质可知：当
时，
随m的增大而增大；当
时，随m的增大而减小
则当
时，取得最大值，最大值为6
此时，
故的面积存在最大值，此时点D坐标为
；
（3）存在．理由如下：
由平行四边形的定义，分以下两种情况讨论：
①当BD是平行四边形的一条边时
如图2所示：M、N分别有三个点
设点
∴点N的纵坐标为绝对值为6
即
解得
（与点D重合，舍去）或
或
则点
的横坐标分别为
∴点M坐标为
或
或
即点M坐标为
或
或
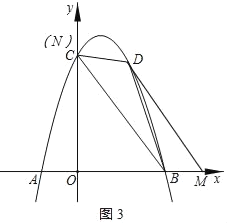
②如图3，当BD是平行四边形的对角线时
∴此时，点N与C重合，
，且点M在点B右侧
，即
综上，存在这样的点M，使得以点
为顶点的四边形是平行四边形．点M坐标为或
或或．
