题目内容
【题目】如图,在ABCD中,∠DAB=60°,点E、F分别在CD、AB的延长线上,且AE=AD,CF=CB.
(1)求证:四边形AFCE是平行四边形;
(2)若去掉已知条件的“∠DAB=60°”,上述的结论还成立吗?若成立,请写出证明过程;若不成立,请说明理由.

【答案】(1)见解析;(2)成立,见解析
【解析】试题分析:(1)由已知条件可得△AED,△CFB是正三角形,可得∠AEC=∠BFC=60°,∠EAF=∠FCE=120°,所以四边形AFCE是平行四边形.
(2)上述结论还成立,可以证明△ADE≌△CBF,可得∠AEC=∠BFC,∠EAF=∠FCE,所以四边形AFCE是平行四边形.
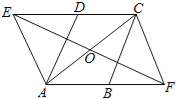
(1)证明:∵四边形ABCD是平行四边形,
∴DC∥AB,∠DCB=∠DAB=60°.
∴∠ADE=∠CBF=60°.
∵AE=AD,CF=CB,
∴△AED,△CFB是正三角形.
∴∠AEC=∠BFC=60°,∠EAF=∠FCE=120°.
∴四边形AFCE是平行四边形.
(2)解:上述结论还成立.
证明:∵四边形ABCD是平行四边形,
∴DC∥AB,∠CDA=∠CBA,∠DCB=∠DAB,AD=BC,DC=AB.
∴∠ADE=∠CBF.
∵AE=AD,CF=CB,
∴∠AED=∠ADE,∠CFB=∠CBF.
∴∠AED=∠CFB.
又∵AD=BC,
在△ADE和△CBF中.
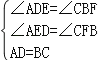 ,
,
∴△ADE≌△CBF(AAS).
∴∠AED=∠BFC,∠EAD=∠FCB.
又∵∠DAB=∠BCD,
∴∠EAF=∠FCE.
∴四边形EAFC是平行四边形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目