题目内容
【题目】已知反比例函数![]() 和一次函数y=2x﹣1,其中一次函数的图象经过(a,b),(a+2,b+k)两点.
和一次函数y=2x﹣1,其中一次函数的图象经过(a,b),(a+2,b+k)两点.
(1)求:反比例函数的解析式.
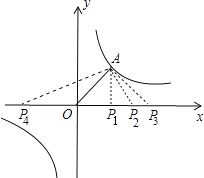
(2)如图,已知点A在第一象限,且同时在上述两函数的图象上.求点A的坐标.
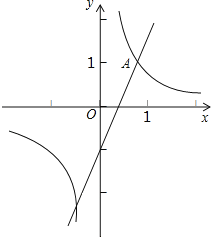
(3)利用(2)的结果,问在x轴上是否存在点P,使得△AOP为等腰三角形?若存在,把符合条件的P点坐标直接写出来;若不存在,说明理由.
【答案】(1)y=![]() ;(2)(1,1);(3)存在,满足条件的点P坐标为( 1,0)、(2,0)、(
;(2)(1,1);(3)存在,满足条件的点P坐标为( 1,0)、(2,0)、(![]() ,0)、(﹣
,0)、(﹣![]() ,0).
,0).
【解析】
试题分析:(1)先把(a,b)、(a+2,b+k)代入y=2x﹣1得到![]() ,然后结果代数式变形可解得k=4,则可确定反比例函数解析式;
,然后结果代数式变形可解得k=4,则可确定反比例函数解析式;
(2)把一次函数与反比例函数解析式组成方程组,再解方程组可确定A点坐标;
(3)先利用勾股计算出OA=![]() ,过A点作AP1⊥x轴,则△OAP1为等腰三角形;作点O关于AP1的对称点P2,则△OAP2为等腰三角形;以O点为圆心,OA为半径画弧交x轴与P3,P4,则△OAP3、△OAP4为等腰三角形;然后利用线段长分别确定各点坐标.
,过A点作AP1⊥x轴,则△OAP1为等腰三角形;作点O关于AP1的对称点P2,则△OAP2为等腰三角形;以O点为圆心,OA为半径画弧交x轴与P3,P4,则△OAP3、△OAP4为等腰三角形;然后利用线段长分别确定各点坐标.
解:(1)把(a,b)、(a+2,b+k)代入y=2x﹣1得![]() ,解得k=4,
,解得k=4,
所以反比例函数解析式为y=![]() ;
;
(2)解方程组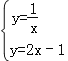 得
得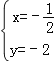 或
或![]() ,
,
∵A点在第一象限,
∴点A的坐标为(1,1);
(3)存在.
OA=![]() =
=![]() ,
,
满足条件的点P坐标为( 1,0)、(2,0)、(![]() ,0)、(﹣
,0)、(﹣![]() ,0).
,0).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目