题目内容
【题目】如图,在△ABC中,AC=BC>AB,点P为△ABC所在平面内一点,且点P与△ABC的任意两个顶点构成△PAB,△PBC,△PAC均是等腰三角形,则满足上述条件的所有点P的个数为 个.
【答案】6.
【解析】
试题分析:根据线段垂直平分线上的点到线段两端点的距离相等,作出AB的垂直平分线,首先△ABC的外心满足,再根据圆的半径相等,以点C为圆心,以AC长为半径画圆,AB的垂直平分线相交于两点,分别以点A、B为圆心,以AC长为半径画圆,与AB的垂直平分线相交于一点,再分别以点A、B为圆心,以AB长为半径画圆,与⊙C相交于两点,即可得解.
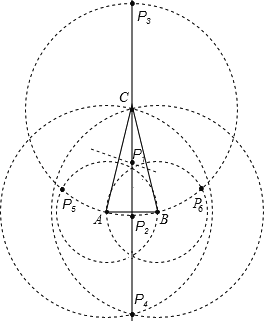
解:如图所示,作AB的垂直平分线,①△ABC的外心P1为满足条件的一个点,
②以点C为圆心,以AC长为半径画圆,P2、P3为满足条件的点,
③分别以点A、B为圆心,以AC长为半径画圆,P4为满足条件的点,
④分别以点A、B为圆心,以AB长为半径画圆,P5、P6为满足条件的点,
综上所述,满足条件的所有点P的个数为6.
故答案为:6.

练习册系列答案
相关题目