题目内容
如图,已知点A(-3,5)在抛物线y=
x2+c的图象上,点P从抛物线的顶点Q出发,沿y轴以每秒 1个单位的速度向正方向运动,连接AP并延长,交抛物线于点B,分别过点A、B作x轴的垂线,垂足为C、D,连接AQ、BQ.
1个单位的速度向正方向运动,连接AP并延长,交抛物线于点B,分别过点A、B作x轴的垂线,垂足为C、D,连接AQ、BQ.
(1)求抛物线的解析式;
(2)当A、Q、B三点构成以AQ为直角边的直角三角形时,求点P离开点Q多少时间?
(3)试探索当AP、AC、BP、BD与一个平行四边形的四条边对应相等(即这四条线段能构成平行四边形)时,点P离开点Q的时刻.
| 1 | 2 |
 1个单位的速度向正方向运动,连接AP并延长,交抛物线于点B,分别过点A、B作x轴的垂线,垂足为C、D,连接AQ、BQ.
1个单位的速度向正方向运动,连接AP并延长,交抛物线于点B,分别过点A、B作x轴的垂线,垂足为C、D,连接AQ、BQ.(1)求抛物线的解析式;
(2)当A、Q、B三点构成以AQ为直角边的直角三角形时,求点P离开点Q多少时间?
(3)试探索当AP、AC、BP、BD与一个平行四边形的四条边对应相等(即这四条线段能构成平行四边形)时,点P离开点Q的时刻.
分析:(1)把点A(-3,5)代入抛物线y=
x2+c,即可求出c的值,从而得二次函数解析式;
(2)根据P为动点以及A、Q、B三点构成以AQ为直角边的直角三角形,分两种情况讨论:①若AQ⊥BQ,过点Q作MQ⊥y轴,可证△AMQ∽△QNB.②若AQ⊥AB,由于AC∥PQ,可证△AMQ∽△QAP,然后根据相似三角形的性质解答;
(3)根据AP、AC、BP、BD与一个平行四边形的四条边对应相等,分三种情况讨论:①AC=BD,AP=BP时,根据轴对称的性质解答;②AC=AP时,利用勾股定理结合一次函数解析式解答.
| 1 |
| 2 |
(2)根据P为动点以及A、Q、B三点构成以AQ为直角边的直角三角形,分两种情况讨论:①若AQ⊥BQ,过点Q作MQ⊥y轴,可证△AMQ∽△QNB.②若AQ⊥AB,由于AC∥PQ,可证△AMQ∽△QAP,然后根据相似三角形的性质解答;
(3)根据AP、AC、BP、BD与一个平行四边形的四条边对应相等,分三种情况讨论:①AC=BD,AP=BP时,根据轴对称的性质解答;②AC=AP时,利用勾股定理结合一次函数解析式解答.
解答:解:(1)把A(-3,5)代入得:5=
×9+c,
∴c=
.
(2)①若AQ⊥BQ,过点Q作MQ⊥y轴,过点Q作QN⊥BD于点N,
可证△AMQ∽△QNB.
∵AM=AC-MC=
,MQ=3,
∴
=
=
.
设B(3k,2k+
),
代入抛物线解析式得:k=
,即B(
,
).
∴直线AB的解析式为:y=-
x+
.
∴OP=
,
∴PQ=2.
②若AQ⊥AB,
∵AC∥PQ,可证△AMQ∽△QAP,
又由勾股定理得AQ=
.
∴PQ=
=
.
∴对应的时刻t为:2或
.
(3)①若AC=BD,AP=BP,
此时点A与点B关于y轴对称,
∴OP=AC=5,
∴PQ=4
.
②若AC=AP,
设P(0,y),则:9+(y-5)2=25,
解之得,y=1,即OP=1.
∴PQ=
.
此时,直线AP解析式为:y=-
x+1.
与抛物线的交点B为(
,
),
∴PB=
=
=BD.
∴满足条件的时刻为:
和4
.
| 1 |
| 2 |
∴c=
| 1 |
| 2 |
(2)①若AQ⊥BQ,过点Q作MQ⊥y轴,过点Q作QN⊥BD于点N,
可证△AMQ∽△QNB.
∵AM=AC-MC=
| 9 |
| 2 |

∴
| BN |
| NQ |
| MQ |
| AM |
| 2 |
| 3 |
设B(3k,2k+
| 1 |
| 2 |
代入抛物线解析式得:k=
| 4 |
| 9 |
| 4 |
| 3 |
| 25 |
| 18 |
∴直线AB的解析式为:y=-
| 5 |
| 6 |
| 5 |
| 2 |
∴OP=
| 5 |
| 2 |
∴PQ=2.
②若AQ⊥AB,
∵AC∥PQ,可证△AMQ∽△QAP,
又由勾股定理得AQ=
3
| ||
| 2 |
∴PQ=
| AQ2 |
| AM |
| 13 |
| 2 |
∴对应的时刻t为:2或
| 13 |
| 2 |
(3)①若AC=BD,AP=BP,
此时点A与点B关于y轴对称,
∴OP=AC=5,
∴PQ=4
| 1 |
| 2 |
②若AC=AP,
设P(0,y),则:9+(y-5)2=25,
解之得,y=1,即OP=1.
∴PQ=
| 1 |
| 2 |
此时,直线AP解析式为:y=-
| 4 |
| 3 |
与抛物线的交点B为(
| 1 |
| 3 |
| 5 |
| 9 |
∴PB=
|
| 6 |
| 9 |
∴满足条件的时刻为:
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查了二次函数解析式的确定、函数图象交点的求法等知识点.主要考查学生数形结合及分类讨论的数学思想方法.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )
如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )A、
| ||||
B、
| ||||
C、2
| ||||
D、4
|
 16、如图,已知点D是∠ABC的平分线上一点,点P在BD上,PA⊥AB,PC⊥BC,垂足分别为A,C、下列结论错误的是( )
16、如图,已知点D是∠ABC的平分线上一点,点P在BD上,PA⊥AB,PC⊥BC,垂足分别为A,C、下列结论错误的是( )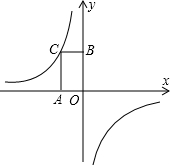 如图,已知点C为反比例函数y=-
如图,已知点C为反比例函数y=- 如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设
如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设 如图,已知点C为AB上一点,AC=12cm,CB=
如图,已知点C为AB上一点,AC=12cm,CB=