题目内容
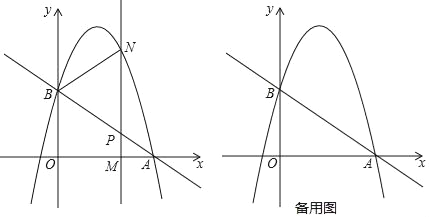
【题目】如图，二次函数y=(x-2)2+m的图象与y轴交于点C，点B是点C关于该二次函数图象的对称轴对称的点，已知一次函数y=kx+b的图象上的点A（1,0）及B.
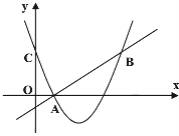
（1）求二次函数与一次函数的解析式；
（2）根据图象，写出满足kx+b≤（x-2）2+m的x的取值范围.
【答案】(1)y=（x-2）2-1，y=x-1;(2) x≤1或x≥4.
【解析】试题分析：（1）将点A的坐标代入二次函数解析式求出m的值，再根据二次函数解析式求出点C的坐标，然后求出点B的坐标，最后利用待定系数法求一次函数解析式求解即可；
（2）根据函数图象点A以及点A左边的部分，点B以及点B右边的部分的自变量x的取值范围即为不等式的解集．
试题解析：（1）将点A（1，0）代入y=（x-2）2+m得（1-2）2+m=0，解得m=-1，
所以二次函数解析式为y=（x-2）2-1；
当x=0时，y=4-1=3，
所以C点坐标为（0，3），
由于C和B关于对称轴对称，而抛物线的对称轴为直线x=2，
所以B点坐标为（4，3），
将A（1，0）、B（4，3）代入y=kx+b得
，
解得
，
所以一次函数解析式为y=x-1；
（2）观察图象可得x的取值范围：x≤1或x≥4.
练习册系列答案
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案
相关题目
