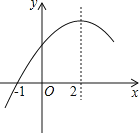题目内容
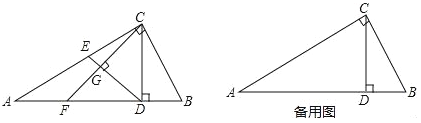
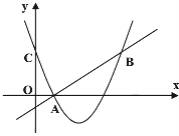
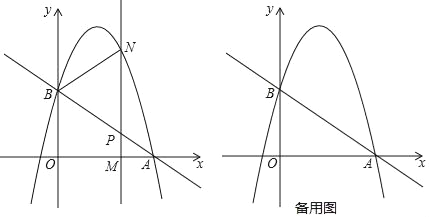
【题目】如图,抛物线y=﹣![]() +bx+c过点A(3,0),B(0,2).M(m,0)为线段OA上一个动点(点M与点A不重合),过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N.
+bx+c过点A(3,0),B(0,2).M(m,0)为线段OA上一个动点(点M与点A不重合),过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N.
(1)求直线AB的解析式和抛物线的解析式;
(2)如果点P是MN的中点,那么求此时点N的坐标;
(3)如果以B,P,N为顶点的三角形与△APM相似,求点M的坐标.
【答案】(1)直线AB的解析式为y=﹣![]() x+2,抛物线解析式为y=﹣
x+2,抛物线解析式为y=﹣![]() x2+
x2+![]() x+2;(2)N点坐标为(
x+2;(2)N点坐标为(![]() ,
, ![]() );(3)点M的坐标为(
);(3)点M的坐标为(![]() ,0)或(
,0)或(![]() ,0).
,0).
【解析】试题分析:(1)运用待定系数法求解即可;
(2设N(m,﹣ ![]() m2+
m2+![]() m+2),P(m,﹣
m+2),P(m,﹣![]() m+2),那么NP=﹣
m+2),那么NP=﹣![]() m2+4m,PM=﹣
m2+4m,PM=﹣![]() m+2,根据NP=PM列方程求解即可;
m+2,根据NP=PM列方程求解即可;
(3)分△BPN∽△OBA和△BPN∽△ABO两种情况,列方程求解.
解:(1)设直线AB的解析式为y=px+q,
把A(3,0),B(0,2)代入得![]() ,解得
,解得![]() ,
,
∴直线AB的解析式为y=﹣![]() x+2;
x+2;
把A(3,0),B(0,2)代入y=﹣![]() +bx+c得
+bx+c得 ,解得
,解得![]() ,
,
∴抛物线解析式为y=﹣![]() x2+
x2+![]() x+2;
x+2;
(2)∵M(m,0),MN⊥x轴,
∴N(m,﹣![]() m2+
m2+![]() m+2),P(m,﹣
m+2),P(m,﹣![]() m+2),
m+2),
∴NP=﹣![]() m2+4m,PM=﹣
m2+4m,PM=﹣![]() m+2,
m+2,
而NP=PM,
∴﹣![]() m2+4m=﹣
m2+4m=﹣![]() m+2,解得m1=3(舍去),m2=
m+2,解得m1=3(舍去),m2=![]() ,
,
∴N点坐标为(![]() ,
,![]() );
);
(3)∵A(3,0),B(0,2),P(m,﹣![]() m+2),
m+2),
∴AB=![]() =
=![]() ,BP=
,BP=![]() =
=![]() m,
m,
而NP=﹣![]() m2+4m,
m2+4m,
∵MN∥OB,
∴∠BPN=∠ABO,
当![]() =
=![]() 时,△BPN∽△OBA,则△BPN∽△MPA,即
时,△BPN∽△OBA,则△BPN∽△MPA,即![]() m:2=(﹣
m:2=(﹣![]() m2+4m):
m2+4m):![]() ,
,
整理得8m2﹣11m=0,解得m1=0(舍去),m2=![]() ,
,
此时M点的坐标为(![]() ,0);
,0);
当![]() =
=![]() 时,△BPN∽△ABO,则△BPN∽△APM,即
时,△BPN∽△ABO,则△BPN∽△APM,即![]() m:
m:![]() =(﹣
=(﹣![]() m2+4m):2,
m2+4m):2,
整理得2m2﹣5m=0,解得m1=0(舍去),m2=![]() ,
,
此时M点的坐标为(![]() ,0);
,0);
综上所述,点M的坐标为(![]() ,0)或(
,0)或(![]() ,0).
,0).

【题目】在互联网技术的影响下,幸福新村的村民小刘在网上销售苹果,原计划每天卖100千克,但实际每天的销量与计划销量相比有出入,如表是某周的销售情况(超额记为正,不足记为负.单位:千克):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
与计划量的差值 |
|
|
|
|
|
|
|
(1)根据表中的数据可知前三天共卖出___________千克;
(2)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售多少千克?
(3)若每千克按5元出售,每千克苹果的运费为1元,那么小刘本周一共收入多少元?