��Ŀ����
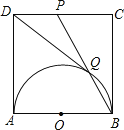
����Ŀ����������������y��![]() ��y��
��y��![]() �ڵ�һ�����ڵ�ͼ����ͼ��ʾ����P��y��
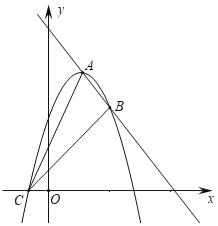
�ڵ�һ�����ڵ�ͼ����ͼ��ʾ����P��y��![]() ��ͼ������PC��x���ڵ�C����y��
��ͼ������PC��x���ڵ�C����y��![]() ��ͼ���ڵ�A��PD��y���ڵ�D����y��
��ͼ���ڵ�A��PD��y���ڵ�D����y��![]() ��ͼ���ڵ�B������P��y��
��ͼ���ڵ�B������P��y��![]() ��ͼ�����˶�ʱ�����½��ۣ��١�ODB���OCA�������ȣ����ı���PAOB��������ᷢ���仯����PA��PBʼ����ȣ��ܵ���A��PC���е�ʱ����Bһ����PD���е㣮����һ����ȷ����(�� ��)
��ͼ�����˶�ʱ�����½��ۣ��١�ODB���OCA�������ȣ����ı���PAOB��������ᷢ���仯����PA��PBʼ����ȣ��ܵ���A��PC���е�ʱ����Bһ����PD���е㣮����һ����ȷ����(�� ��)
A. �٢ڢ� B. �ڢۢ� C. �٢ڢ� D. �٢ۢ�
���𰸡�C
��������
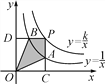
�����ڵ�A�͵�D����ͬһ������������![]() ��ͼ����,����S��ODB=
��ͼ����,����S��ODB=![]() ,S��OCA=
,S��OCA=![]()
,�ʡ�ODB���OCA��������,�ʱ�ѡ����ȷ,�ڸ��ݷ����������ļ�������,�ı���PAOB�����ʼ�յ���|k|-1,�ʱ�ѡ����ȷ,����ͼ��֪,��OC��ODʱ,PA��PB,�ʱ�ѡ�����,�����ڷ�������������Գ�ͼ��,��AΪPC���е�ʱ,BΪPD���е�,�ʱ�ѡ����ȷ,��ѡC.

��ϰ��ϵ�д�
 ����ѵ�����⿼ϵ�д�
����ѵ�����⿼ϵ�д�
�����Ŀ