题目内容
【题目】已知二次函数y=kx2+ ![]() x+
x+ ![]() (k是常数).
(k是常数).
(1)若该函数的图象与x轴有两个不同的交点,试求k的取值范围;
(2)若点(1,k)在某反比例函数图象上,要使该反比例函数和二次函数y=kx2+ ![]() x+
x+ ![]() 都是y随x的增大而增大,求k应满足的条件及x的取值范围;
都是y随x的增大而增大,求k应满足的条件及x的取值范围;
(3)若抛物线y=kx2+ ![]() x+
x+ ![]() 与x轴交于A(xA , 0)、B(xB , 0)两点,且xA<xB , xA2+xB2=34,若与y轴不平行的直线y=ax+b经过点P(1,3),且与抛物线交于Q1(x1 , y1)、Q2(x2 , y2)两点,试探究
与x轴交于A(xA , 0)、B(xB , 0)两点,且xA<xB , xA2+xB2=34,若与y轴不平行的直线y=ax+b经过点P(1,3),且与抛物线交于Q1(x1 , y1)、Q2(x2 , y2)两点,试探究 ![]() 是否为定值,并写出探究过程.
是否为定值,并写出探究过程.
【答案】
(1)
解:∵二次函数y=kx2+ ![]() x+
x+ ![]() 与x轴有两个不同的交点,
与x轴有两个不同的交点,
∴ 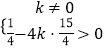 ,
,
解得k< ![]() 且k≠0.
且k≠0.
(2)
解:设反比例函数解析式为y= ![]() ,
,
∵经过点(1,k),
∴m=k,
∵反比例函数和二次函数y=kx2+ ![]() x+
x+ ![]() 都是y随x的增大而增大,
都是y随x的增大而增大,
∴k<0,
x<﹣ ![]() ,即x<﹣
,即x<﹣ ![]()
(3)
解:结论: ![]() =1.
=1.
理由:令y=0,则有kx2+ ![]() x+
x+ ![]() =0,
=0,
∴xA+xB=﹣ ![]() ,xAxB=
,xAxB= ![]() ,
,
∵xA2+xB2=34,
∴(xA+xB)2﹣2xAxB=34,
∴( ![]() )2﹣
)2﹣ ![]() ﹣34=0,
﹣34=0,
解得k=﹣ ![]() 或
或 ![]()
由(1)可知k< ![]() ,
,
∴k=﹣ ![]() ,
,
∴抛物线解析式为y=﹣ ![]() x2+
x2+ ![]() x+
x+ ![]() ,
,
设过点P的直线为y=kx+b,把P(1,3)代入得3=k+b,
∴b=3﹣k,
∴过点P的直线为y=kx+3﹣k,
∵过点P的直线为y=kx+3﹣k与物线交于Q1
∴y1=kx1+3﹣k,y2=kx2+3﹣k,
由 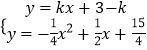 消去y得x2+(4k﹣2)x﹣3﹣4k=0,
消去y得x2+(4k﹣2)x﹣3﹣4k=0,
∴x1+x2=﹣(4k﹣2),x1x2=﹣3﹣4k,
∴ ![]() =
= ![]()
= ![]()
= ![]()
= ![]()
=1.
【解析】(1)根据题意k≠0,△>0,列出不等式组即可解决问题.(2)设反比例函数解析式为y= ![]() ,因为经过点(1,k),所以m=k,再根据条件即可确定k的值以及x的范围.(3)结论:
,因为经过点(1,k),所以m=k,再根据条件即可确定k的值以及x的范围.(3)结论: ![]() =1.令y=0,则有kx2+
=1.令y=0,则有kx2+ ![]() x+
x+ ![]() =0,所以xA+xB=﹣
=0,所以xA+xB=﹣ ![]() ,xAxB=
,xAxB= ![]() ,根据xA2+xB2=34,列出方程求出k的值,设过点P的直线为y=kx+3﹣k,
,根据xA2+xB2=34,列出方程求出k的值,设过点P的直线为y=kx+3﹣k,
由由 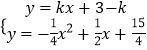 消去y得x2+(4k﹣2)x﹣3﹣4k=0,得x1+x2=﹣(4k﹣2),x1x2=﹣3﹣4k,根据
消去y得x2+(4k﹣2)x﹣3﹣4k=0,得x1+x2=﹣(4k﹣2),x1x2=﹣3﹣4k,根据 ![]() =
= ![]() ,代入化简即可解决问题.
,代入化简即可解决问题.
【考点精析】本题主要考查了二次函数的图象和二次函数的性质的相关知识点,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案





