题目内容
【题目】在正方形ABCD中,AB=AD,∠BAD=90°,P是CD边上一点,连结PA,分别过点B,D作BE⊥PA,DF⊥PA,垂足分别为点E,F,如图①

(1)求证:BE=DF+EF;
(2)若点P在DC的延长线上,如图②,上述结论还成立吗?如果成立请写出证明过程;如果不成立,请写出正确结论并加以证明.
(3)若点P在CD的延长线上,如图③,那么这三条线段的数量关系是 .(直接写出结果)
【答案】(1)详见解析;(2)上述结论不成立,正确结论为:DF=EF+BE;(3)EF=BE+DF.
【解析】
(1)由BE垂直于AP,DF垂直于AP,得到一对直角相等,再由四边形ABCD为正方形,得到AB=AD,且∠BAD为直角,利用同角的余角相等得到一对角相等,利用AAS得到三角形ABE与三角形DFA全等,利用全等三角形对应边相等得到BE=AF,AE=DF,根据AF-AE=EF,等量代换即可得证;
(2)在图②中BE、DF、EF这三条线段长度具有这样的数量关系:DF=EF+BE,理由同(1);
(3)在图③中BE、DF、EF这三条线段长度具有这样的数量关系:EF=BE+DF,理由同(1).
(1)证明:∵BE⊥PA,DF⊥PA,
∴∠BEA=∠AFD=90°,
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∴∠BAE+∠DAF=90°,
又∵∠AFD=90°,
∴∠ADF+∠DAF=90°,
∴∠BAE=∠ADF,
在△BAE和△ADF中,
∵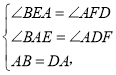
∴△BAE≌△ADF(AAS),
∴BE=AF,AE=DF,
∵AF=EF+AE,
∴BE=DF+EF.
(2)上述结论不成立,正确结论为:DF=EF+BE;
∵BE⊥PA,DF⊥PA,
∴∠BEA=∠AFD=90,
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∴∠BAE+∠DAF=90°,
又∵∠AFD=90,
∴∠ADF+∠DAF=90,
∴∠BAE=∠ADF,
在△BAE和△ADF中,

∴△BAE≌△ADF(AAS),
∴BE=AF,AE=DF,
∵AE =EF+AF,
∴DF =EF+BE.
(3)EF=BE+DF.
理由为:∵BE⊥PA,DF⊥PA,
∴∠BEA=∠AFD=90°,
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∴∠BAE+∠DAF=90°,
又∵∠AFD=90°,
∴∠ADF+∠DAF=90°,
∴∠BAE=∠ADF,
在△BAE和△ADF中,
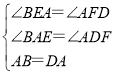
∴△BAE≌△ADF(AAS),
∴BE=AF,AE=DF,
∵AE+AF=EF,
∴EF=BE+DF.