题目内容
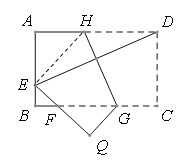
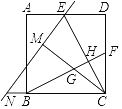
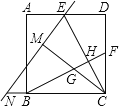
【题目】如图,在正方形ABCD中,E,F分别为AD,CD的中点,BF与CE相交于点H,直线EN交CB的延长线于点N,作CM⊥EN于点M,交BF于点G,且CM=CD,有以下结论:①BF⊥CE;②ED=EM;③tan∠ENC=![]() ;④S四边形DEHF=4S△CHF,其中正确结论的个数为()
;④S四边形DEHF=4S△CHF,其中正确结论的个数为()
A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】
①正确.由△CDE≌△BCF,推出∠CBF=∠ECD,由∠ECD+∠ECB=90°,推出∠CBF+∠BCE=90°,推出∠BHC=90°,推出BF⊥CE;
②正确.只要证明Rt△CEM≌Rt△CED即可;
③正确.首先证明NE=NC,设NE=CN=x,EM=DE=AE=a,则CM=CD=2a,在Rt△CNM中,可得(x-a)2+(2a)2=x2,推出![]() 由
由![]() 计算即可;
计算即可;
④正确.易知△CHF∽△CDE,可得![]()
∵四边形ABCD是正方形,
∴![]()
∵![]()
∴DE=CF,
∴△CDE≌△BCF,
∴∠CBF=∠ECD,
∵![]()
∴![]()
∴![]()
∴BF⊥CE,故①正确,
∵![]()
∴Rt△CEM≌Rt△CED,
∴EM=DE,故②正确,
∴∠CED=∠CEM=∠ECN,
∴NE=NC,设NE=CN=x,EM=DE=AE=a,则CM=CD=2a,
在Rt△CNM中,![]()
解得![]()
tan∠ENC![]() 故③正确,
故③正确,
易知△CHF∽△CDE,
∴![]()
∴S四边形DEHF=4S△CHF,故④正确,
故选:D.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目