题目内容
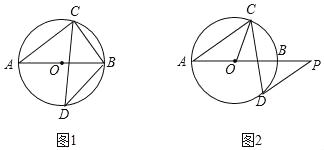
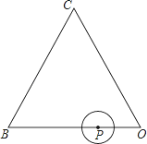
【题目】如图,等边三角形OBC的边长为10,点P沿O→B→C→O的方向运动,⊙P的半径为![]() . ⊙P运动一圈与△OBC的边相切________次,每次相切时,点P到等边三角形顶点最近距离是________.
. ⊙P运动一圈与△OBC的边相切________次,每次相切时,点P到等边三角形顶点最近距离是________.
【答案】6 2
【解析】
分析图形,确定⊙P在运动过程中与各边相切时的情况,从而确定相切次数;
根据切线的性质,由切线与圆的半径垂直,等边三角形的各内角为60°,确定每次相切时,点P的位置,利用三角函数的知识求出⊙P与各边相切时切点与相邻顶点的距离,问题即可解答.
在点P的运动过程中,⊙P依次与OC、BC、BO、CO、BC、OB相切,故⊙P运动一圈与△OBC的边相切6次.
当⊙P与OC相切时,如图所示,过点P作PA⊥CO,则![]()

∵△OBC是等边三角形,
∴∠COP=60°.
∴OP=PA÷sin60°=2.
同理可得:⊙P与BC相切时BP=2,⊙P与BO相切时BP=2,⊙P与CO第二次相切时,CP=2,⊙P与BC第二次相切时CP=2,⊙P与OB第二次相切时OP=2.
综上可得:⊙P与△OBC的边相切时,点P的位置分别是OP=2(点P在OB或OC上);PB=2(点P在OB或BC上);PC=2(点P在BC或OC上).
故答案为:6,2.

【题目】甲、乙两台机床同时生产一种零件,在5天中,两台机床每天出次品的数量如下表:
甲 | 0 | 1 | 2 | 0 | 2 |
乙 | 2 | 1 | 0 | 1 | 1 |
关于以上数据的平均数、中位数、众数和方差,说法不正确的是
A. 甲、乙的平均数相等B. 甲、乙的众数相等
C. 甲、乙的中位数相等D. 甲的方差大于乙的方差
【题目】如图,在△ABC中,∠ACB=90°,∠CAB=30°, AC=4.5cm. M是边AC上的一个动点,连接MB,过点M作MB的垂线交AB于点N. 设AM=x cm,AN=y cm.(当点M与点A或点C重合时,y的值为0)
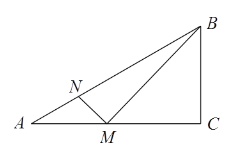
探究函数y随自变量x的变化而变化的规律.
(1) 通过取点、画图、测量,得到了x与y的几组对应值,如下表:
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 |
y/cm | 0 | 0.4 | 0.8 | 1.2 | 1.6 | 1.7 | 1.6 | 1.2 | 0 |
(要求:补全表格,相关数值保留一位小数)
(2)建立平面直角坐标系xOy,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:当AN=![]() AM时,AM的长度约为 cm(结果保留一位小数).
AM时,AM的长度约为 cm(结果保留一位小数).