Question

【题目】一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发， 到达目的地后停止，设慢车行驶时间为 x 小时，两车之间的距离为 y 千米，两者的关系如图 所示：

(1)两车出发 小时后相遇;

(2)求快车和慢车的速度;

(3)求线段 BC 所表示的 y 与 x 的 关系式，并求两车相距 300 千米时的时间.

Answer 1

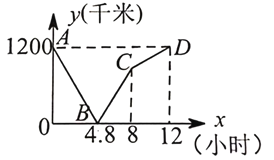
【答案】（1）4.8；（2）150，100；（3）y=250x-1200（4.8≤x≤8），3.6或6

【解析】

（1）根据图象可知两车出发4.8小时相遇；
（2）根据图象和题意可以分别求出慢车和快车的速度；
（3）根据题意可以求得点C的坐标，由图象可以得到点B的坐标，从而可以得到线段BC所表示的y与x之间的函数关系式，再把y=300代入求出对应的y值即可得出两车行驶6小时两车相距多少千米．

解：（1）由图知：两车出发4.8小时相遇；
故答案为：4.8
（2）快车8小时到达，慢车12小时到达，
故：快车速度为1200÷8=150（千米/时），
慢车速度为1200÷12=100（千米/时）；
（3）由题可得，点C是快车刚到达乙地，
∵点C的横坐标是8，
∴纵坐标是：100×8=800，
即点C的坐标为（8，800）．
设线段BC对应的函数解析式为y=kx+b，
∵点B（4.8，0），点C（8，800），

解得：

∴线段BC所表示的y与x的函数关系式是y=250x-1200（4.8≤x≤8）．
当y=300时，300=250x-1200，解得x=6．

设线段AB对应的函数解析式为y1=k1x+b1，

点B（4.8，0），点A（0，1200）

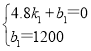解得：

线段AB所表示的y与x的函数关系式是y1=-250x+1200（0≤x≤4.8）;

当y=300时，300=-250x+1200，解得x=3.6．
即两车相距300千米时的时间为3.6或6时．