题目内容
矩形的两条对角线夹角为120°,矩形的宽为3,则矩形的面积是( )
A.
| B.3
| C.6
| D.9
|
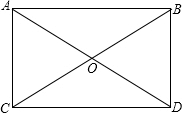
如下图所示:四边形ABDC是对角线夹角为120°的矩形,即:∠COD=120°,AC=3,
∵四边形ABDC是矩形,且∠COD=120,
∴∠AOC=180°-∠COD=60°,∠ACD=90°,∠CAD=∠AOC=∠ACO=60°,
在Rt△ACD中,
CD=AC×tan60°=3
,
所以,矩形的面积为:AC×CD=3×3
=9
.
故选D.
∵四边形ABDC是矩形,且∠COD=120,
∴∠AOC=180°-∠COD=60°,∠ACD=90°,∠CAD=∠AOC=∠ACO=60°,
在Rt△ACD中,
CD=AC×tan60°=3
| 3 |
所以,矩形的面积为:AC×CD=3×3
| 3 |
| 3 |
故选D.


练习册系列答案
相关题目

 AB=
AB=




