题目内容
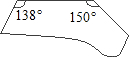
梯形的两底角之和为90°，上底长为3，下底长为7，连接两底中点的线段的长是（ ）
| A．2 | B．3 | C．4 | D．5 |
如图，过E作EG∥AB交BC于G，作EH∥CD交BC于H，
∴∠EGF=∠B，∠EHF=∠C，
∵∠B+∠C=90°，
∴∠EGF+∠EHF=90°，
∴∠GEH=90°，
∵点E、F分别是AD、BC的中点，
∴AE=ED=BG=CH，
∴GF=FH，
∵AD=3，BC=7，
∴GH=7-3=4，
∴EF=
GH=2．
∴∠EGF=∠B，∠EHF=∠C，
∵∠B+∠C=90°，
∴∠EGF+∠EHF=90°，
∴∠GEH=90°，
∵点E、F分别是AD、BC的中点，
∴AE=ED=BG=CH，
∴GF=FH，
∵AD=3，BC=7，
∴GH=7-3=4，
∴EF=
| 1 |
| 2 |
练习册系列答案
全能测控期末小状元系列答案
相关题目
，0），C（6，2
