题目内容

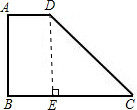
如图，直角梯形中∠B=90°，AD∥BC，AB=BC=8，CD=10，则梯形的面积是______平方单位．
作DE⊥BC
∵∠B=90°
∴AB∥DE．
又∵AD∥BC
∴四边形ABED是矩形
∴AD=BE，AB=DE
∴在Rt△DEC中，CD=10，DE=AB=8，根据勾股定理得CE=
CD2-DE2
=
102-82
=6
∴BE=BC-CE=8-6=2
∴AD=2
∴S梯形ABCD=
1
2
（AD+BC）×AB=
1
2
×（2+2+6）×8=40．
练习册系列答案
相关题目
若等腰梯形的上底、高、下底分别为2cm、2cm、6cm，则这个等腰梯形中的锐角等于______．
如图，在平面直角坐标系中，等腰梯形AOBC的四个顶点坐标分别为A（2，2
3
），O（0，0），B（8，0），C（6，2
3
）．
（1）求等腰梯形AOBC的面积；
（2）试说明点A在以OB的中点D为圆心，OB为直径的圆上；
（3）在第一象限内确定点M，使△MOB与△AOB相似，求出所有符合条件的点M的坐标．
如图1，AB、CD是两条线段，M是AB的中点，S△DMC、S△DAC、S△DBC分别表示△DMC、△DAC、△DBC的面积．当AB∥CD时，则有S△DMC=
S△DAC+S△DBC
2
．
（1）如图2，M是AB的中点，AB与CD不平行时，作AE、MN、BF分别垂直DC于E、N、F三个点，问结论①是否仍然成立？请说明理由．
（2）若图3中，AB与CD相交于点O时，问S△DMC、S△DAC和S△DBC三者之间存在何种相等关系？试证明你的结论．
如图所示，在直角梯形ABCD中，AD∥BC，∠A=90°，AB=12，BC=21，AD=16．动点P从点B出发，沿射线BC的方向以每秒2个单位长的速度运动，动点Q同时从点A出发，在线段AD上以每秒1个单位长的速度向点D运动，当其中一个动点到达端点时另一个动点也随之停止运动．设运动的时间为t（秒）．
（1）当t为何值时，四边形PQDC的面积是梯形ABCD的面积的一半；
（2）四边形PQDC能为平行四边形吗？如果能，求出t的值；如果不能，请说明理由．
（3）四边形PQDC能为等腰梯形吗？如果能，求出t的值；如果不能，请说明理由．
如图，在梯形ABCD中，AD∥BC，AB=AD=DC=2cm，BC=4cm，在等腰△PQR中，∠QPR=120°，底边QR=6cm，点B、C、Q、R在同一直线l上，且C、Q两点重合，如果等腰△PQR以1cm/秒的速度沿直线l箭头所示方向匀速运动，t秒时梯形ABCD与等腰△PQR重合部分的面积记为S平方厘米．
（1）当t=4时，求S的值；
（2）当4≤t≤10，求S与t的函数关系式，并求出S的最大值．
等腰梯形的下底与上底之差等于它的腰长，则这个梯形的各内角度数为______．
如图（1），直角梯形OABC中，∠A=90°，AB∥CO，且AB=2，OA=2
3
，∠BCO=60°．
（1）求证：△OBC为等边三角形；
（2）如图（2），OH⊥BC于点H，动点P从点H出发，沿线段HO向点O运动，动点Q从点O出发，沿线段OA向点A运动，两点同时出发，速度都为1/秒．设点P运动的时间为t秒，△OPQ的面积为S，求S与t之间的函数关系式，并求出t的取值范围；
（3）设PQ与OB交于点M，当OM=PM时，求t的值．
下列四个图形缺口都能与右边的图形缺口吻合，哪个图形有可能与右边残缺的图形拼成一个梯形（　　）
A．B．C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网