题目内容
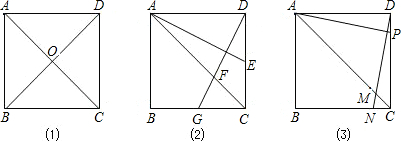
(1)如图(1),在正方形ABCD中,对角线AC、BD相交于点O,易知AC⊥BD,
=
;
(2)如图(2),若点E是正方形ABCD的边CD的中点,即
=
,过D作DG⊥AE,分别交AC、BC于点F、G.求证:
=
;
(3)如图(3),若点P是正方形ABCD的边CD上的点,且
=
(n为正整数),过点D作DN⊥AP,分别交AC、BC于点M、N,请你先猜想CM与AC的比值是多少,然后再证明你猜想的结论.
| CO |
| AC |
| 1 |
| 2 |
(2)如图(2),若点E是正方形ABCD的边CD的中点,即
| DE |
| DC |
| 1 |
| 2 |
| CF |
| AC |
| 1 |
| 3 |
(3)如图(3),若点P是正方形ABCD的边CD上的点,且
| DP |
| DC |
| 1 |
| n |

(2)证明:∵四边形ABCD为正方形,
∴AD=DC,
∴∠1+∠ADG=90°,
又∵DG⊥AE,
∴∠2+∠ADG=90°,
∴∠1=∠2,
∵AD=DC,∠1=∠2,∠ADE=∠DCG=90°,
∴△ADE≌△DCG(ASA),
∴CG=DE,
又∵E为BC中点,
∴CG=DE=
DC,
∴CG=
AD,
∵BC∥AD,
∴
=
=
,
∴
=
;(8分)
(3)猜想
=
;(10分)
同理可证
=
=
,
又∵BC∥AD,
∴
=
=
,
∴
=
.(14分)

∴AD=DC,
∴∠1+∠ADG=90°,
又∵DG⊥AE,
∴∠2+∠ADG=90°,
∴∠1=∠2,
∵AD=DC,∠1=∠2,∠ADE=∠DCG=90°,
∴△ADE≌△DCG(ASA),
∴CG=DE,
又∵E为BC中点,
∴CG=DE=
| 1 |
| 2 |
∴CG=
| 1 |
| 2 |
∵BC∥AD,
∴
| CG |
| AD |
| CF |
| AF |
| 1 |
| 2 |
∴
| CF |
| AC |
| 1 |
| 3 |
(3)猜想
| CM |
| AC |
| 1 |
| n+1 |
同理可证
| CN |
| BC |
| DP |
| DC |
| 1 |
| n |
又∵BC∥AD,
∴
| CM |
| AM |
| CN |
| AD |
| 1 |
| n |
∴
| CM |
| AC |
| 1 |
| n+1 |


练习册系列答案
相关题目